利用 PostgreSQL/PostGIS 扩展模块对空间网络数据连通关系进行管理，能够利用
pgRouting实现对路网、河流网、铁路网等典型空间网络数据及几何拓扑数据的常见功能分析。

要求

1. 能够利用 pgRouting
   实现对路网、河流网、铁路网等典型空间网络数据进行拓扑分析；
2. 能够解决拓扑关系创建过程中的拓扑“gap”、“Insections”等问题；
3. 掌握 pgRouting
   最短路径分析用法，能够自定义函数实现任意两点或多点之间的路径查询；
4. 能够根据掌握 pgRouting 解决生活中实际常见路径分析问题。

任务 1：简单道路网分析及路径查询（无向）

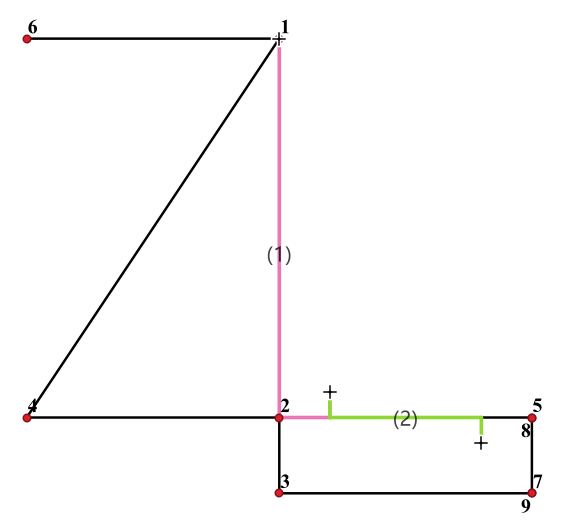
有如下道路网，涵盖 A、B、C、D、E 等 5 个线路；

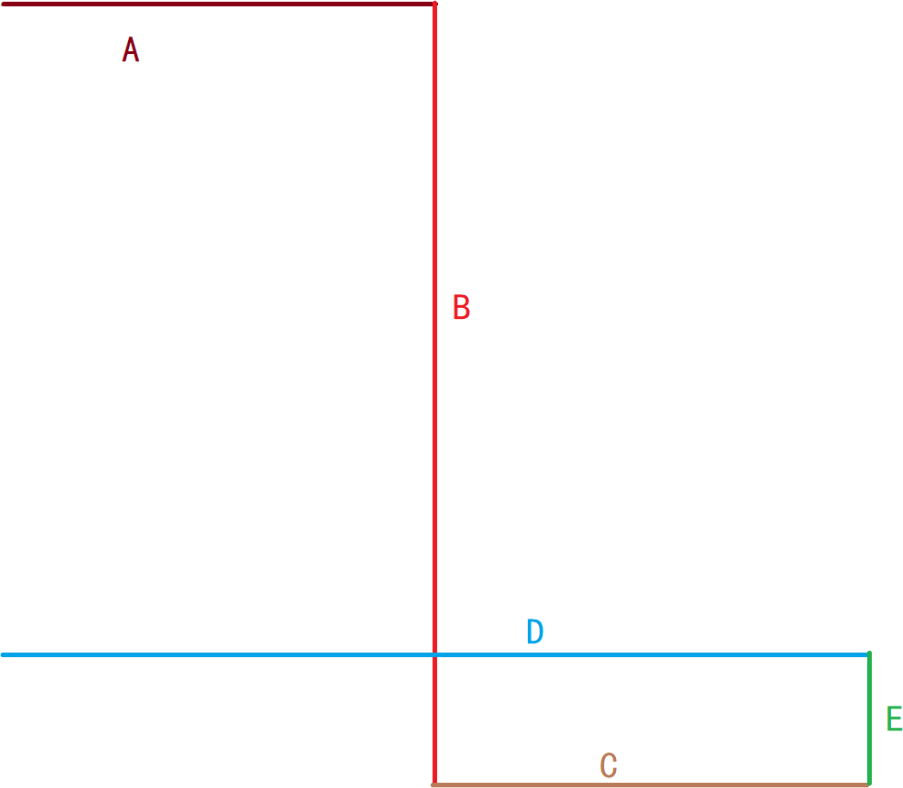
其关系表、几何坐标及参考系如下所示：

1、创建上述道路网拓扑关系，不允许有 gap 和intersection 等异常。

Answer：

创建一个新的数据库，并加载postgis和pgRouting扩展；

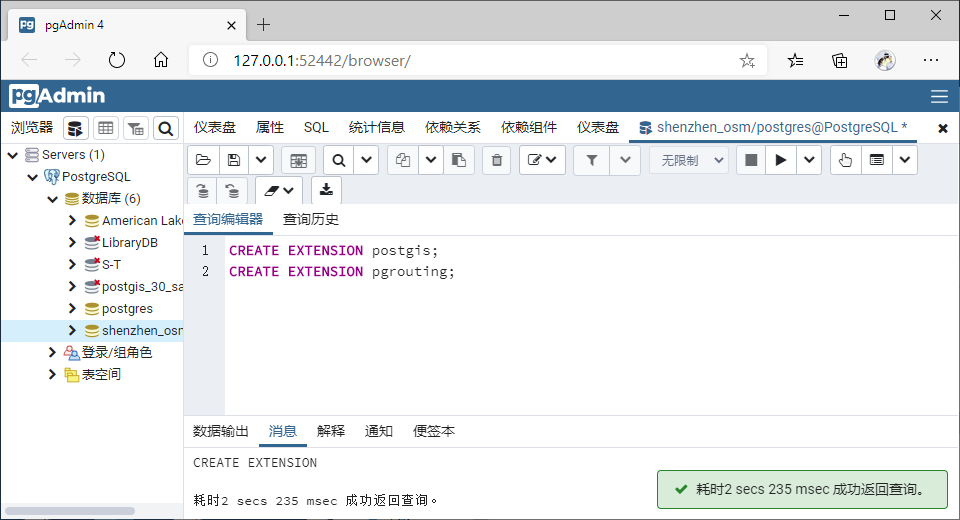
创建Roadtest_Network表，并导入路网数据，并更新长度；

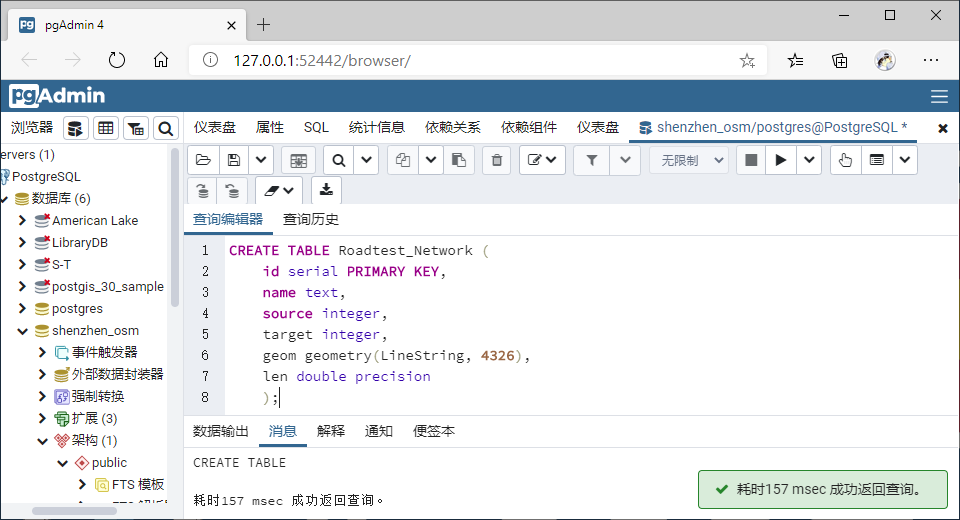
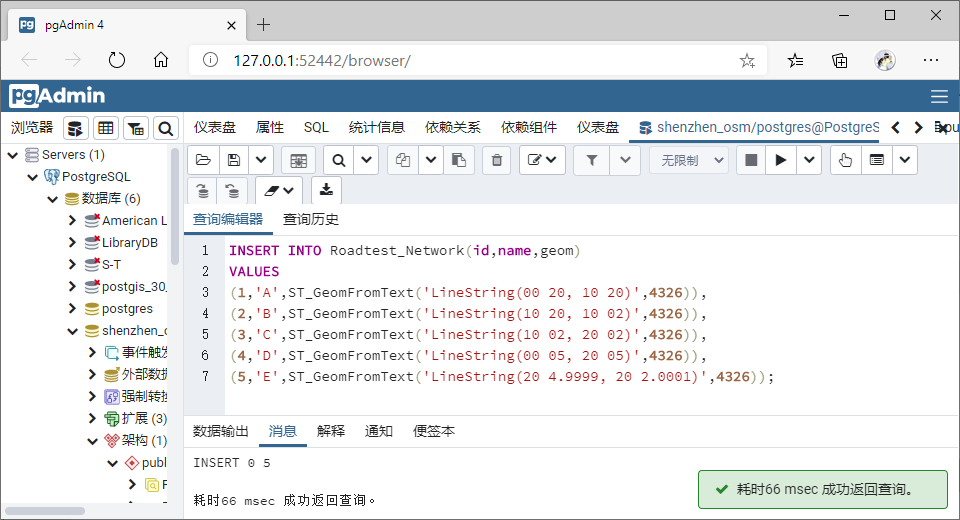
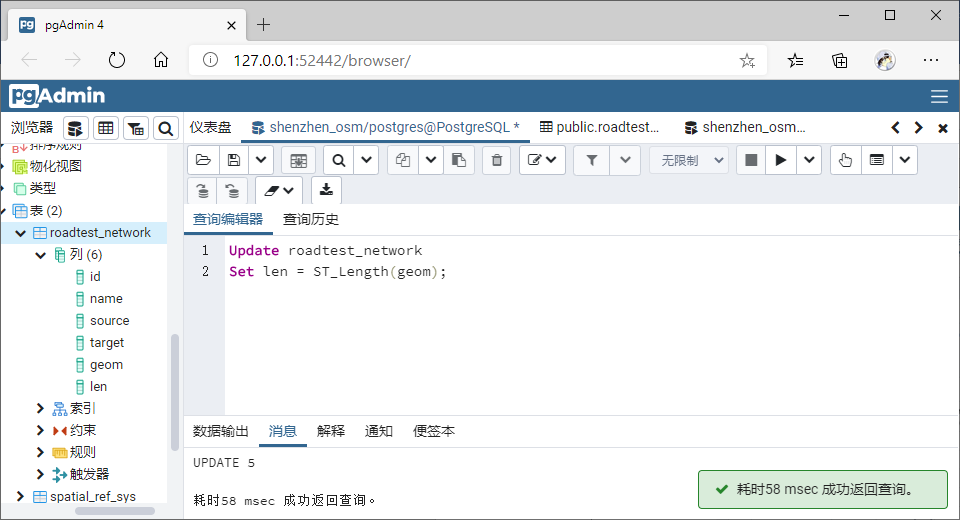
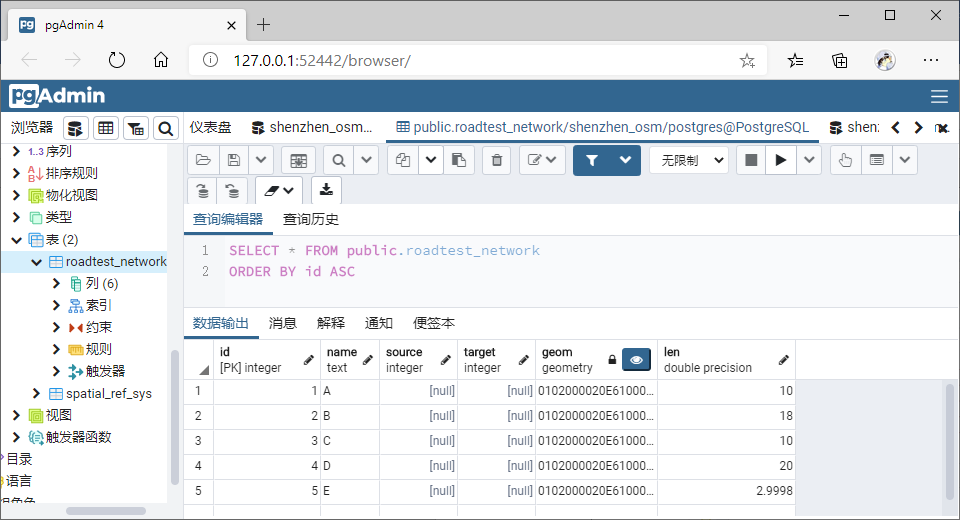
Step1：创建的 Roadtest_Network 表：属性有：id（PK）、name、
source、target、geom、len（作为无向图路段通过的耗时成本）等，并插入相关信息；【该表用以存储网络关系】。表内容信息如下：

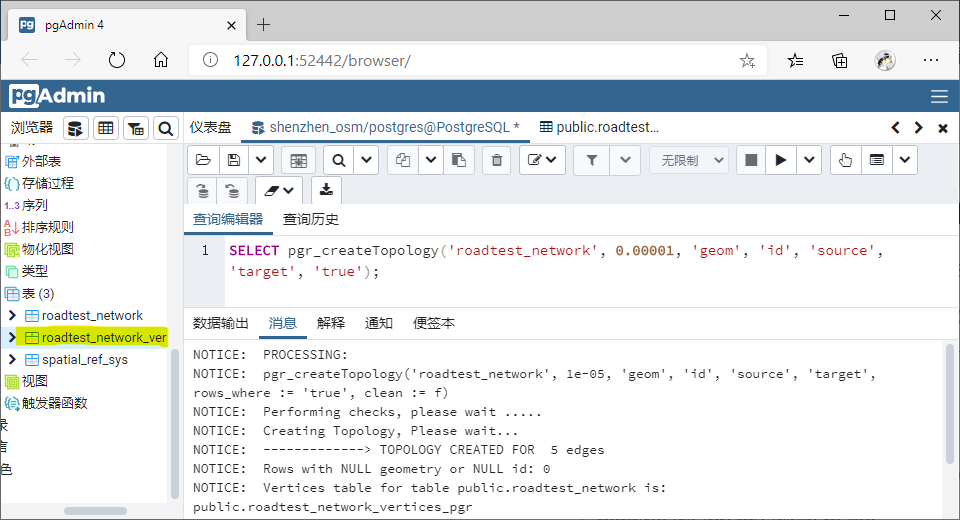
Step2：在 Roadtest_Network 表创建拓扑关系：

输出日志：创建了 5 条边拓扑，生成一个节点表*_vertices_pgr

Roadtest_Network 表中 source 和 target 已被节点填充；

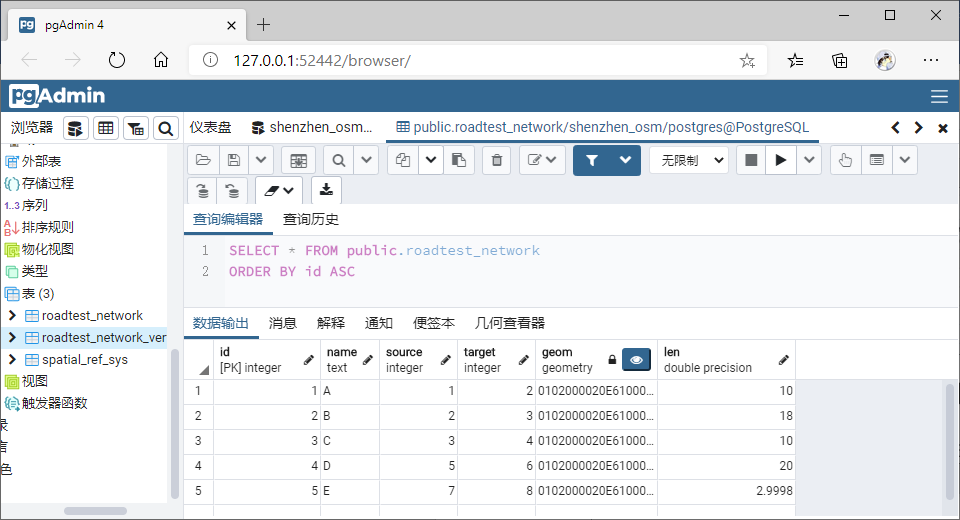
同时，节点表存储所有拓扑节点，但属性 cnt（当前节点被使用的次数）等为空；

采用拓扑分析函数分析“边”和“节点”表，更新相关属性信息，
同时分析已创建拓扑关系有没有异常信息：

检查成功，但该拓扑关系存在一个“相交”问题：

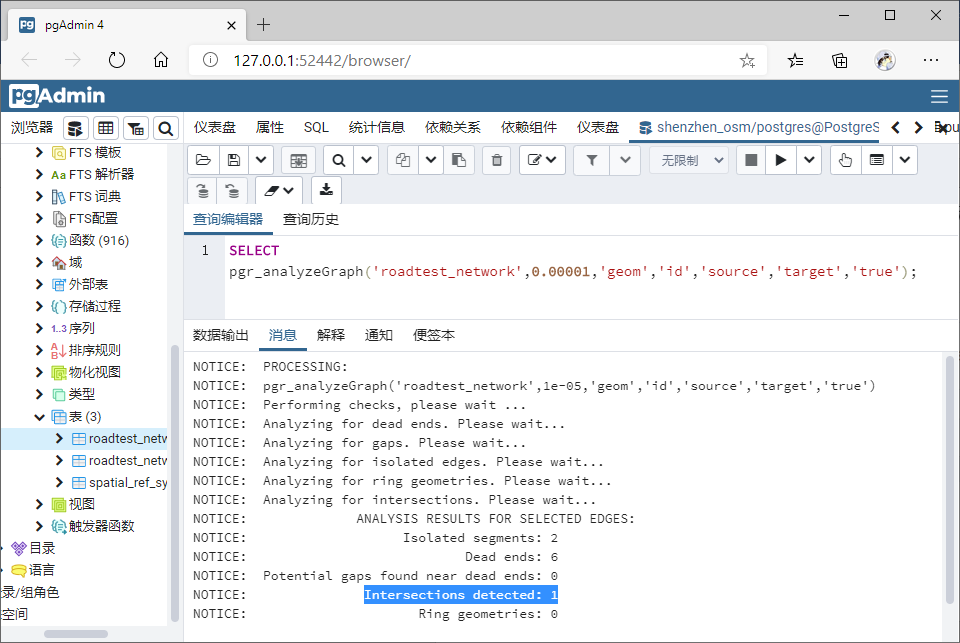
同时“节点”表 cnt（当前节点被使用的次数）属性已更新：

QGIS 中查看“节点”表：

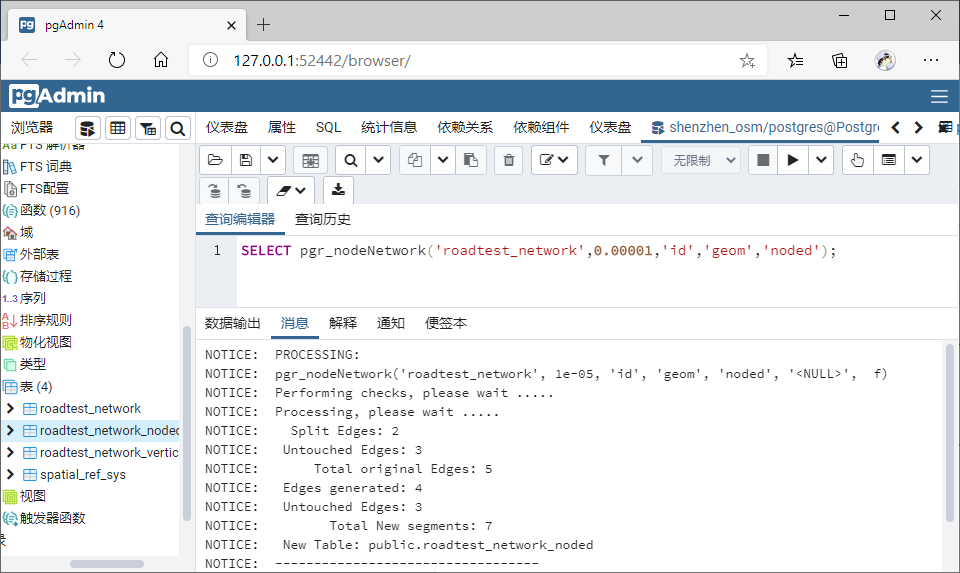
**Step3：**用节点重构函数 pgr_nodeNetwork 重构节点表，避免存在“相交”问题：

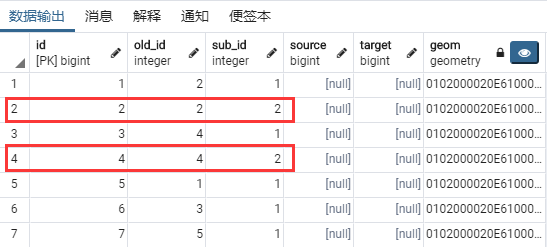
可以看出：重构后将 2（B）和 4（D）两条线段分别分割成 2 条线。

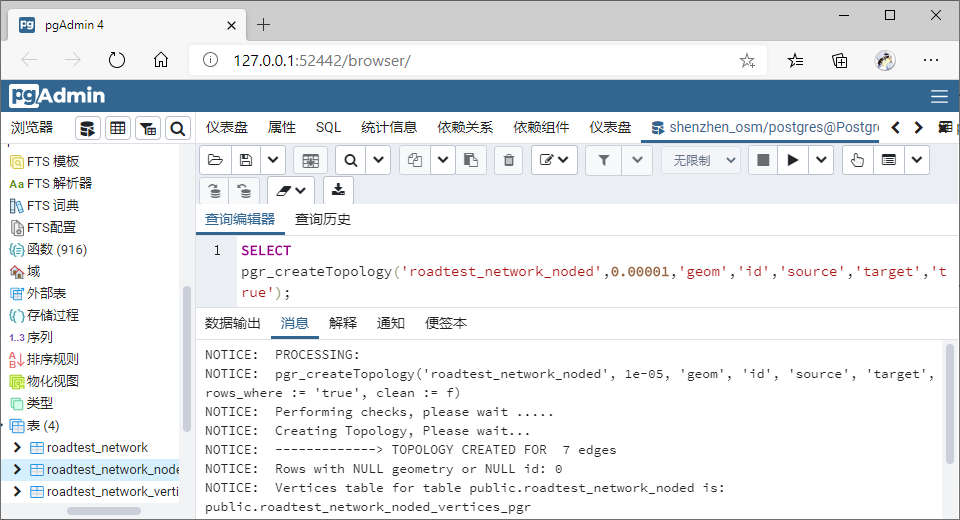
Step4：基于 Roadtest_network_noded 表重建拓扑关系：

节点表：

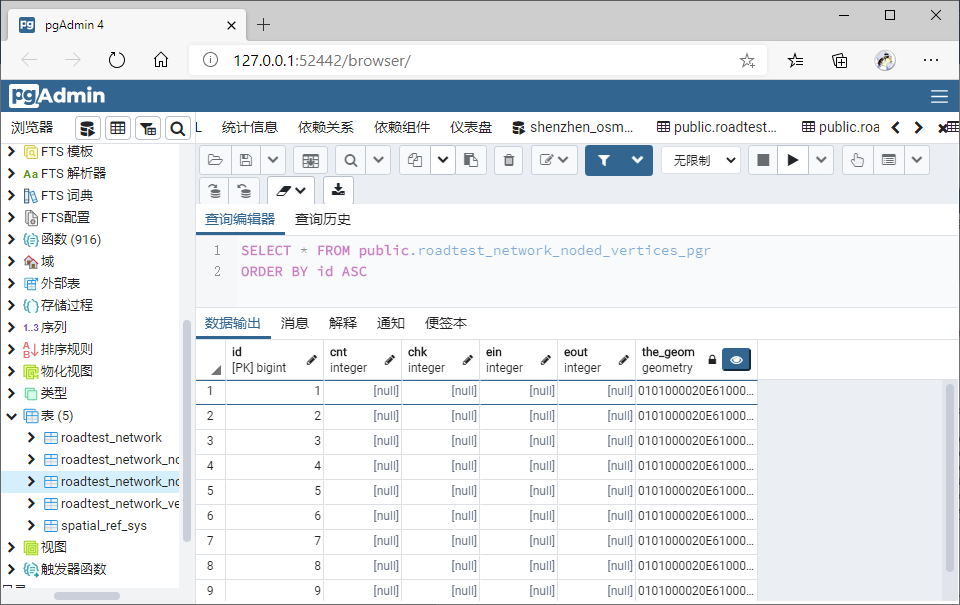
检查拓扑关系：

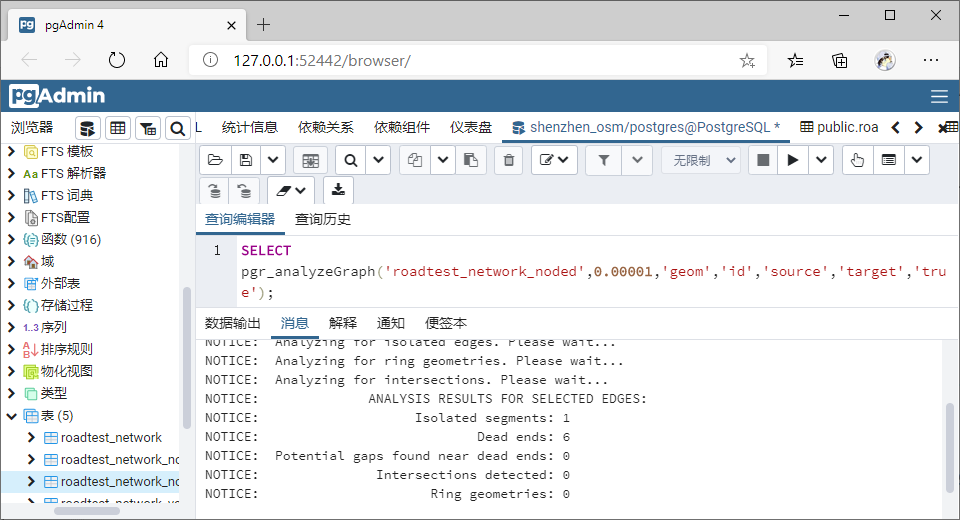
QGIS 查看重构拓扑之后的图示意：

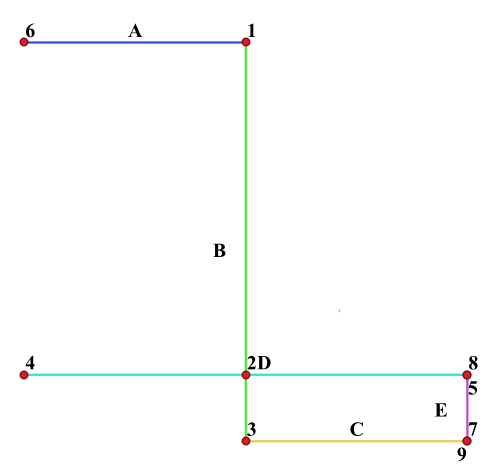
2、新增加路
F，从(0,5)到(10,20)，重新拓扑分析，后将“边”与“节点”关系重新排列，按 ID
顺序排放，方便最短路径查询，重排后如下：

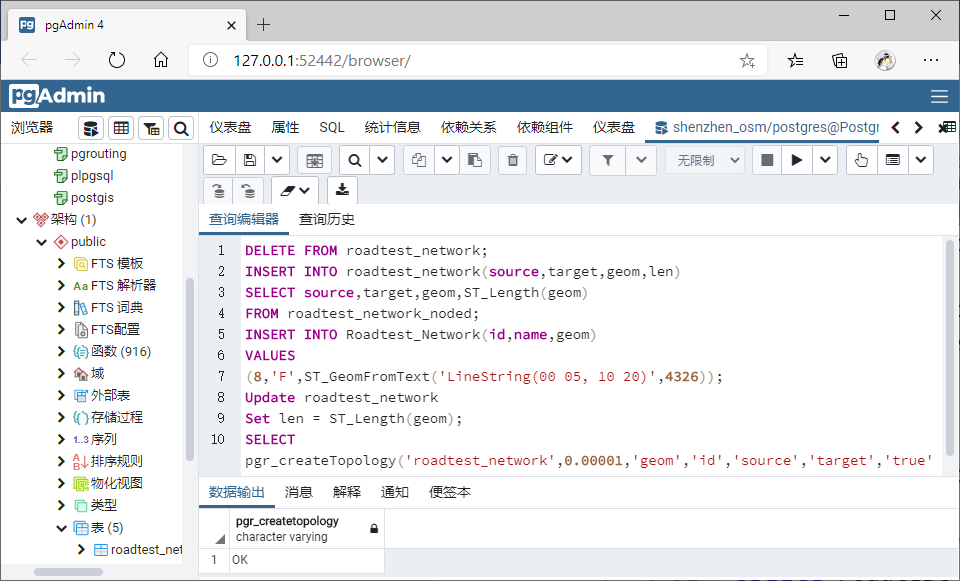
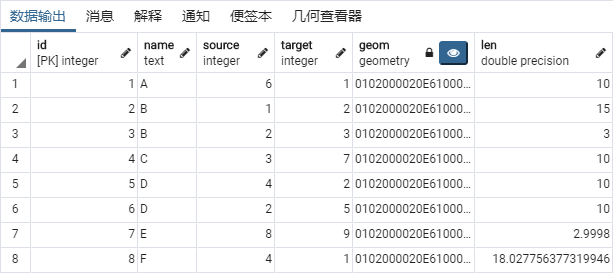
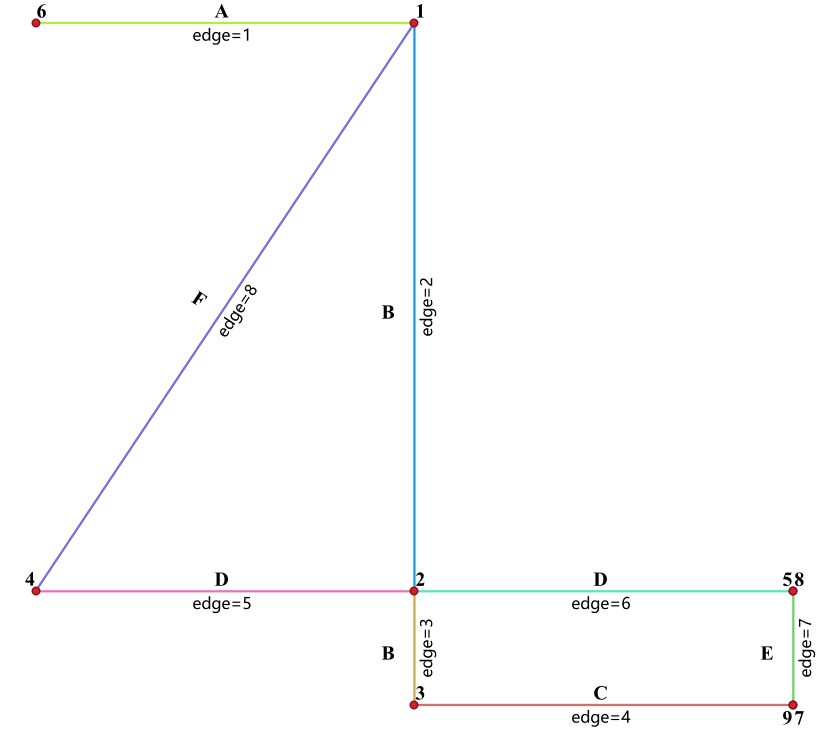
根据上述拓扑关系，完成以下查询：

（1）查询节点 5 至 3 的最短路径；

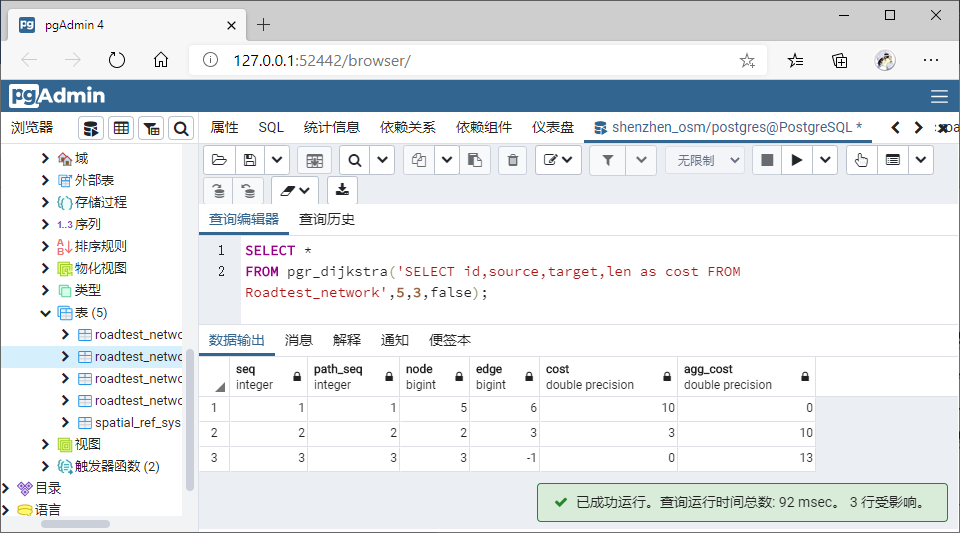
（2）查询(12,6)到(10,20)的最短距离，查询(12,6)到(18,4)的最短距离；

创建自定义函数

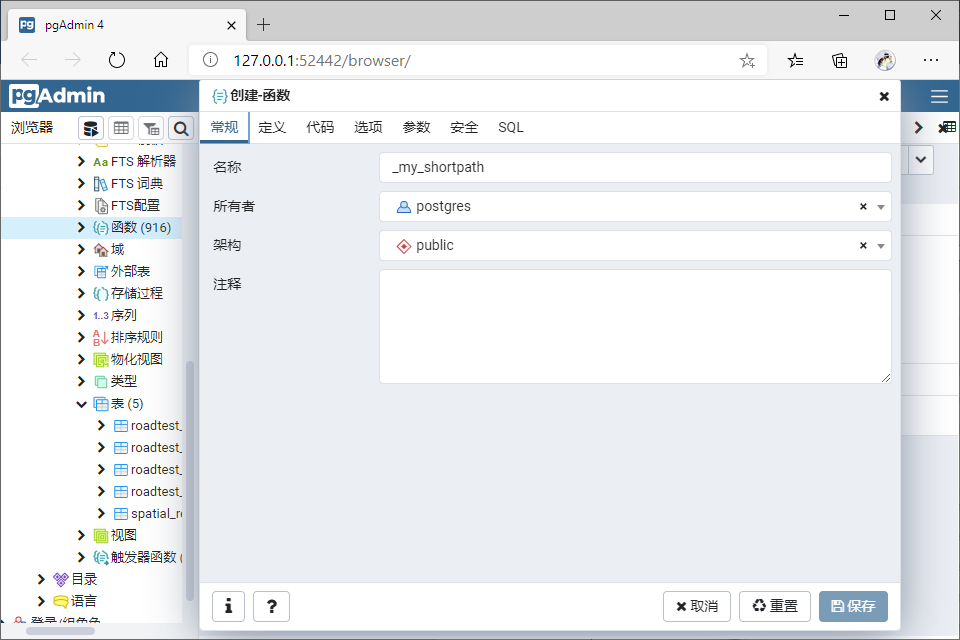
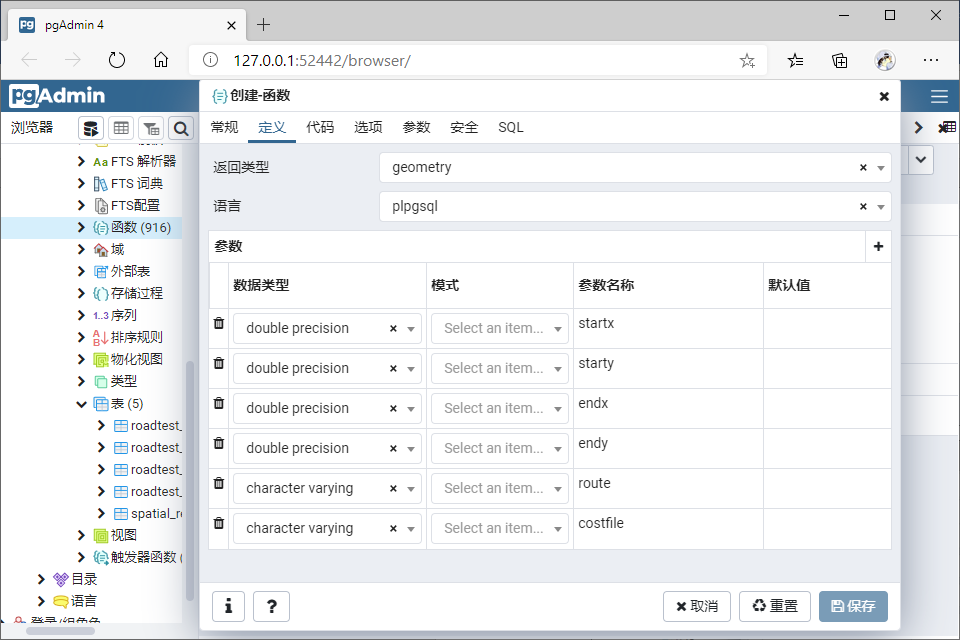
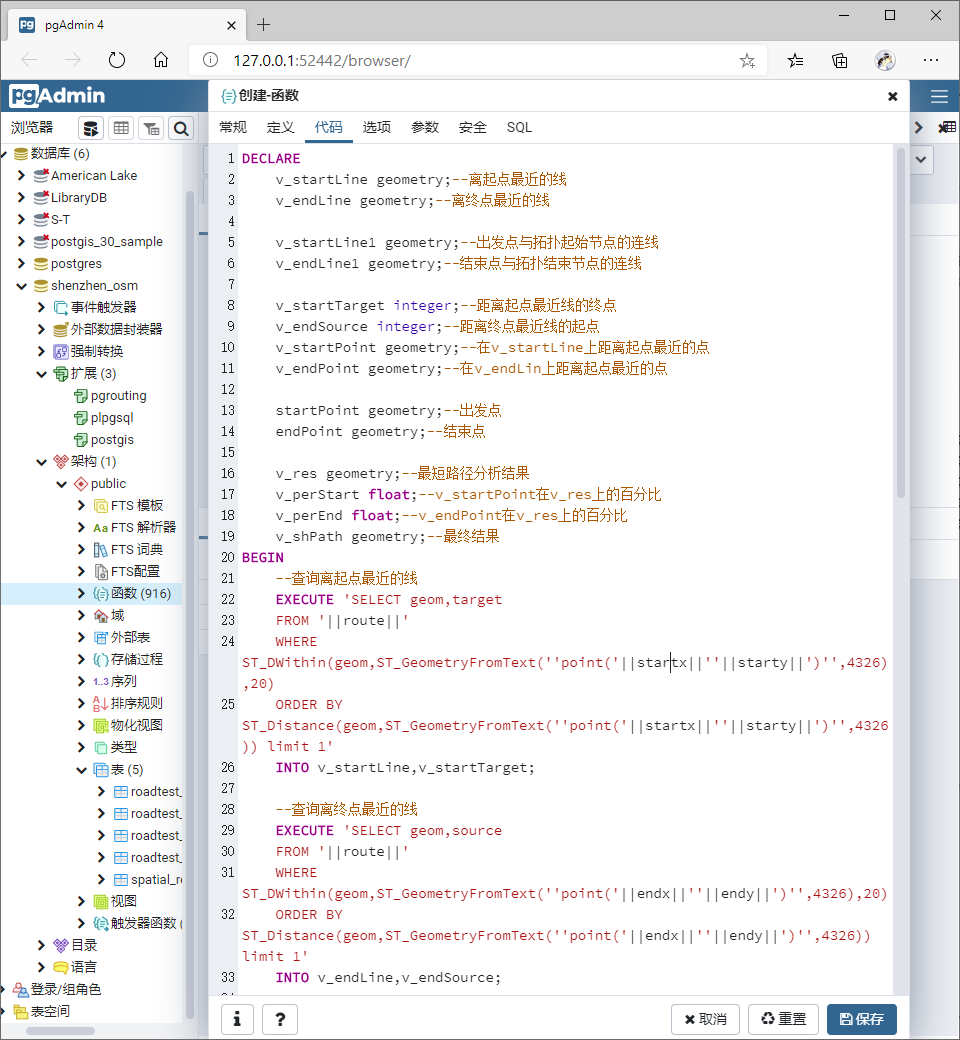
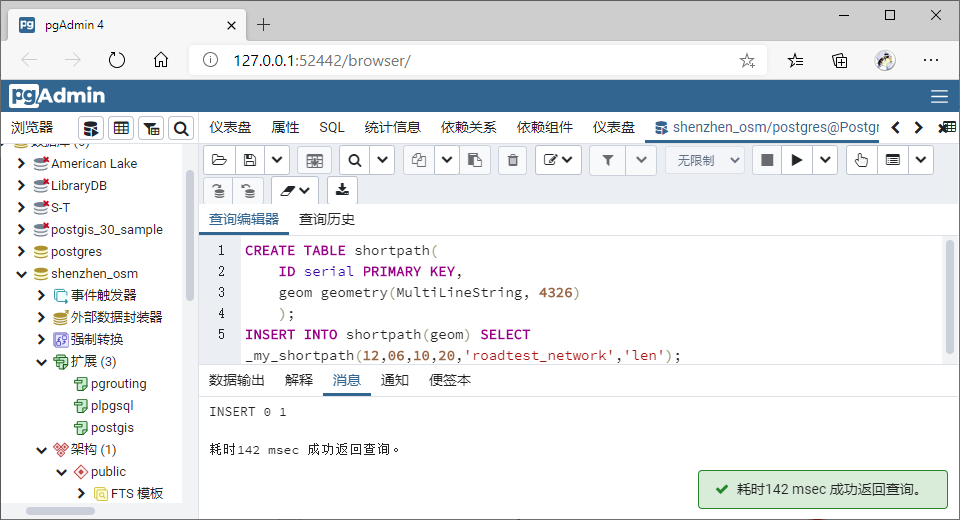
1. 查询(12,6)到(10,20)的最短距离

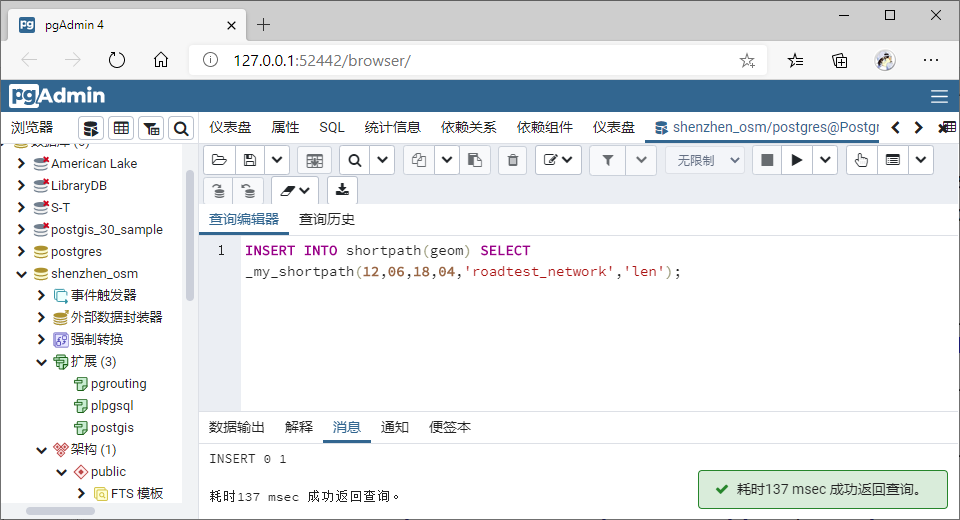
1. 查询(12,6)到(18,4)的最短距离；

在QGIS中展示结果

任务 2：深圳市道路网最短路径查询（双向）

1、实验数据准备

首先要下载 OpenStreetMap 中国地区数据，下载地址：Geofabrik Download Server

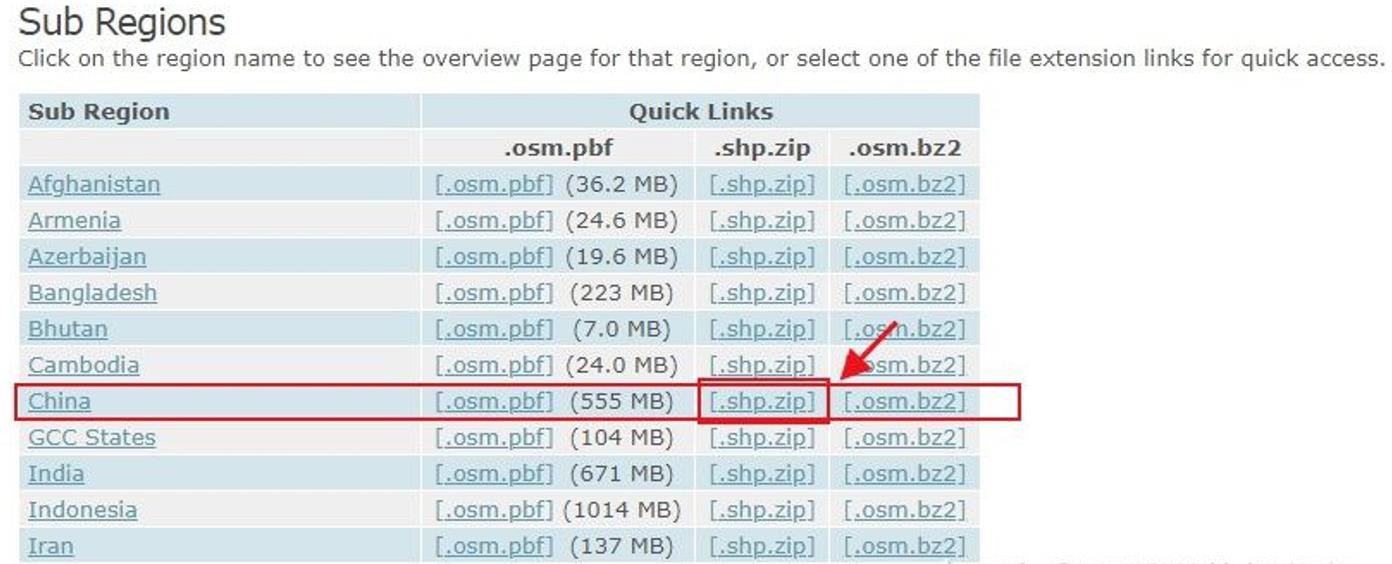
方式一：下载 shapefile 格式数据，然后裁剪出深圳范围的路网数据；

方式二：下载 OSM 格式数据，通过osm2pgsql-1.2.1-x64 工具将OSM
数据导入PostgresSQL；

**注：**由于 OSM 数据是WGS84 坐标系（EPSG:4326）的，所以还需将其转换为 Web
墨卡托坐标系（EPSG:3857)。另外还需要使用ArcGIS
中的"要素转线"这个工具将折线数据在相交点处打断：

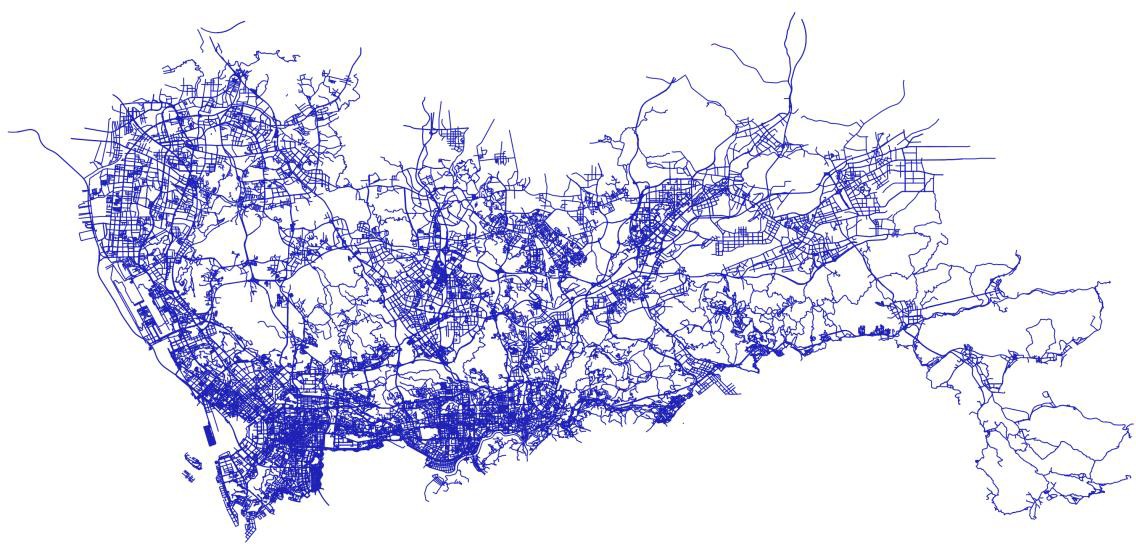
深圳市道路网数据如下所示：

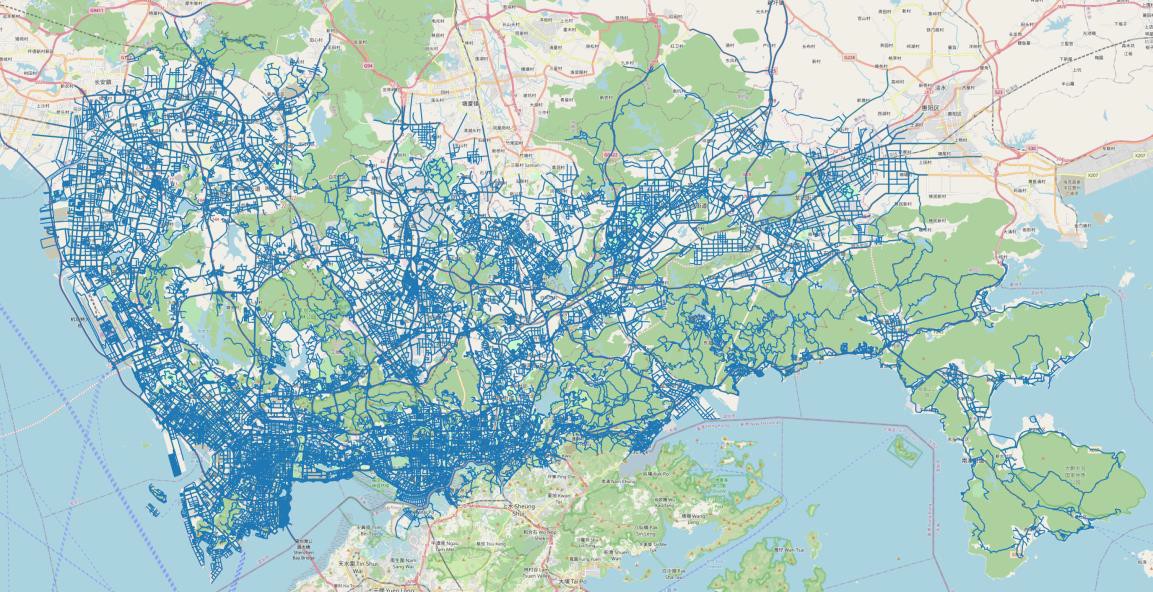
2、将数据导入数据库

2.1创建数据库

做任务1时已经创建并已加载两个扩展

2.2使用 PostGIS 的数据导入工具导入数据

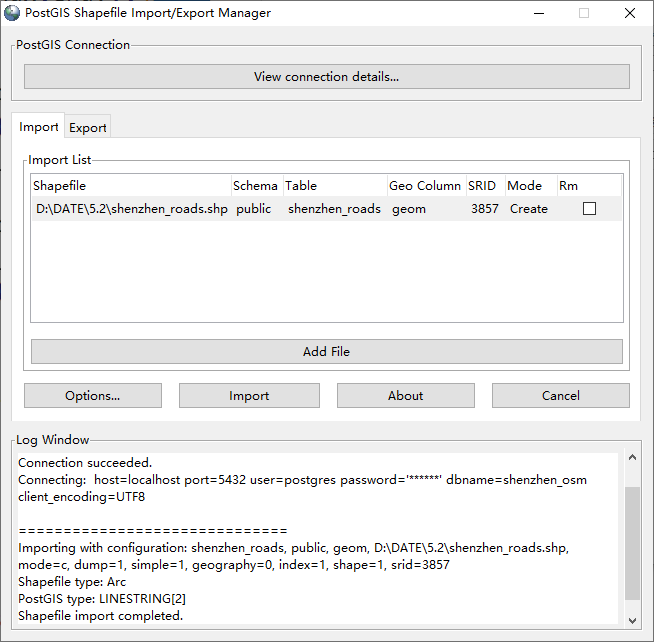
3、设置路径成本并建立路网拓扑

3.1设置路径成本

首先为shenzhen_roads 表添加四个字段：

• source —— 用于保存路径起始顶点的id

• target —— 用于保存路径终止顶点的id

• cost —— 用于保存路径正向的成本（或者代价）

• reverse_cost —— 用于保存路径反向的成本（或者代价）

SQL 语句：

ALTER TABLE shenzhen_roads

ADD COLUMN source INTEGER,

ADD COLUMN target INTEGER,

ADD COLUMN cost DOUBLE PRECISION,

ADD COLUMN reverse_cost DOUBLE PRECISION;

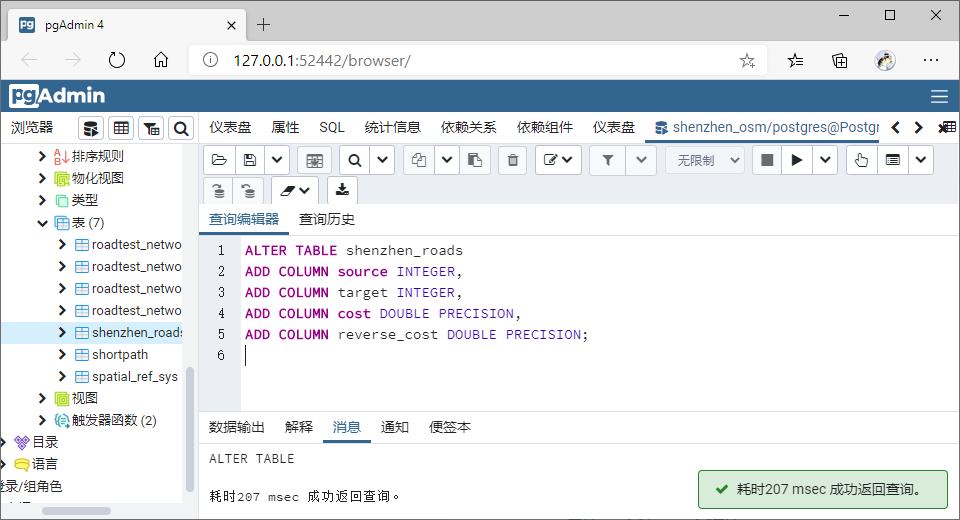
OSM 数据包含一个 oneway 列，它的值可能是以下三个值之一：

• 'F' —— 表示该路径是单向的，且路径方向是正向的。

• 'T' —— 表示该路径是单向的，且路径方向是反向的。

• 'B' —— 表示该路径是双向的。

现在就根据路径的方向来计算各个路径的成本。

将路径的长度作为成本，如果路径是正向的，则 cost 值为路径的长度，reverse_cost
值为-1；如果路径是反向的，则 reverse_cost 值为路径的长度，cost
值为-1；如果路径是双向的，则 cost 和reverse_cost 的值都为路径的长度。

①正向路径的成本：

UPDATE shenzhen_roads

SET cost = ST_Length(geom),

reverse_cost **= -**1

WHERE oneway = 'F';

②反向路径的成本：

UPDATE shenzhen_roads

SET cost = -1,

reverse_cost = ST_Length(geom)

WHERE oneway = 'T';

③双向路径的成本：

UPDATE shenzhen_roads

SET cost = ST_Length(geom),

reverse_cost = ST_Length(geom)

WHERE oneway = 'B';

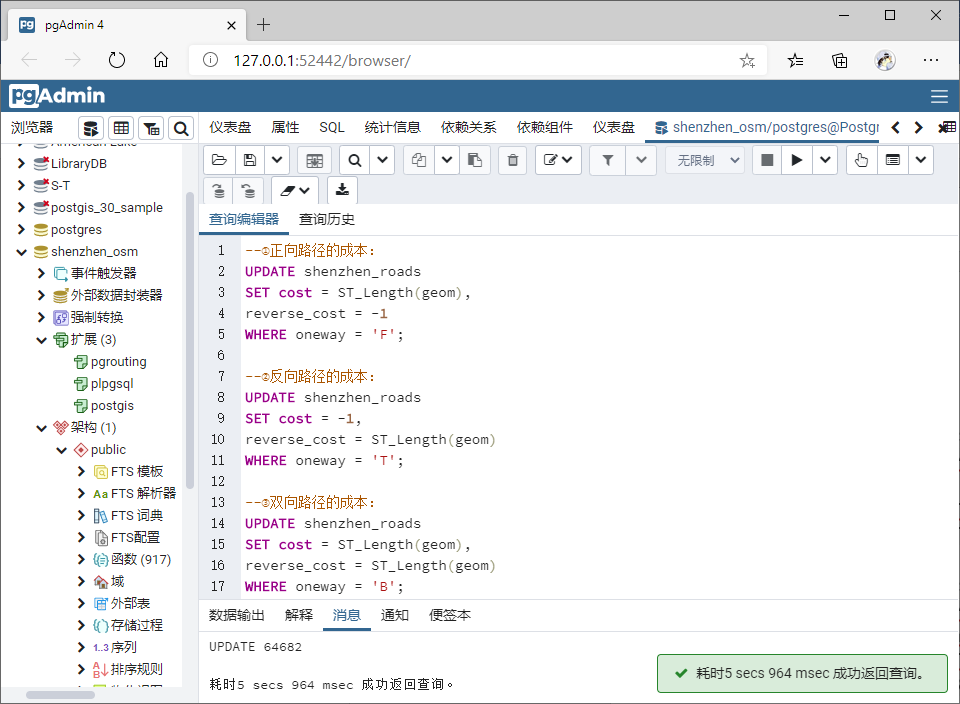
3.2创建路网拓扑

**Key1:**创建路网拓扑需要调用 pgr_createTopology 函数：

SELECT pgr_createTopology(

'shenzhen_roads',

0.001,

'geom',

'gid',

'source',

'target'

);

上面的六个参数分别表示：

• 路网表

• 路径之间的容差，两条路径的距离大于这个容差值，就表示它们不相交（拓扑不捕获节点）。

• 包含几何图形信息的列

• 路网表的主码列

• 保存路径起始顶点的 id 的列

• 保存路径终止顶点的 id 的列

拓扑路径创建完成后，下图日志表明“深圳道路”网拓扑边 111185 条 ， 同 时 数 据 库
中 会 自 动 多 出 一 张 “ 拓 扑 节 点 ”
表shenzhen_roads_vertices_pgr，存储该拓扑边关系的所有“节点”：

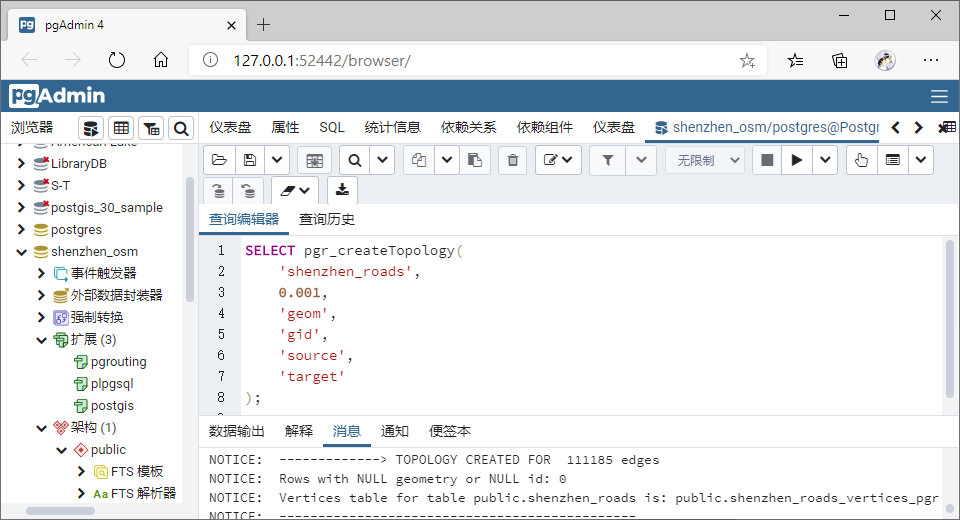
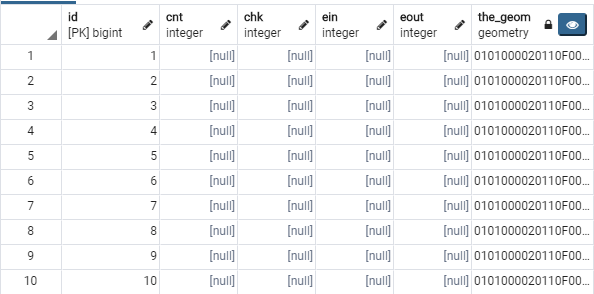
同时所有拓扑路径边的起始、终止顶点数据信息更新在了shenzhen_roads 表中：

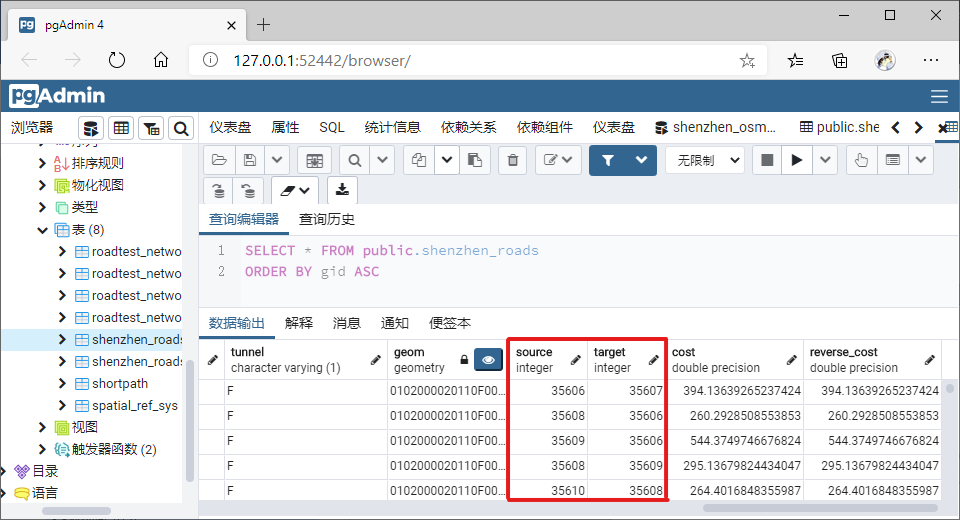
Key2:拓扑检查：通过拓扑检查函数检查该拓扑关系是否存在异常问题，如下图所示，该拓扑关系并“gap”、“Intersections”等异常，无需节点重构。

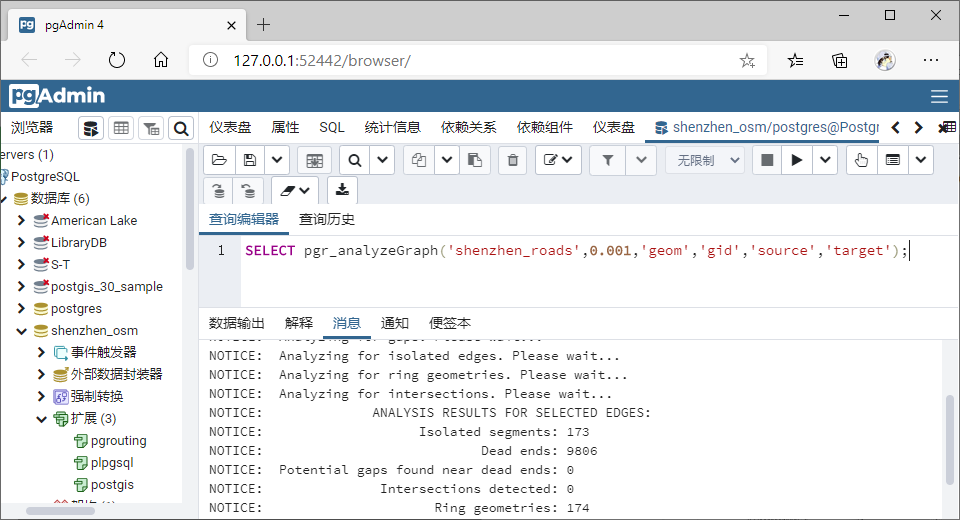
同时节点表cnt（当前）

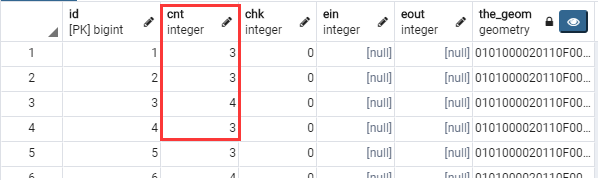
与路网一起可视化显示：

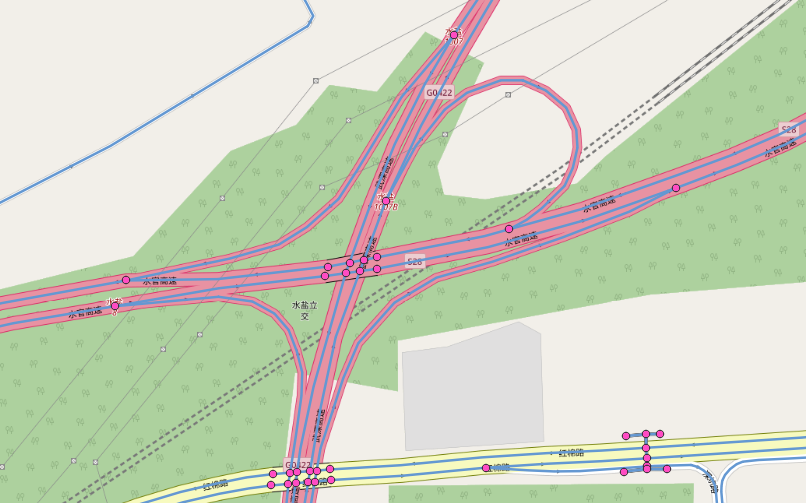
4、最短路径查询

清华大学深圳研究院（ID：59005）

中科院深圳先进技术研究院（ID：59193）

塘朗山郊野公园西北（ID：57059）

塘朗山郊野公园东（ID：16177）

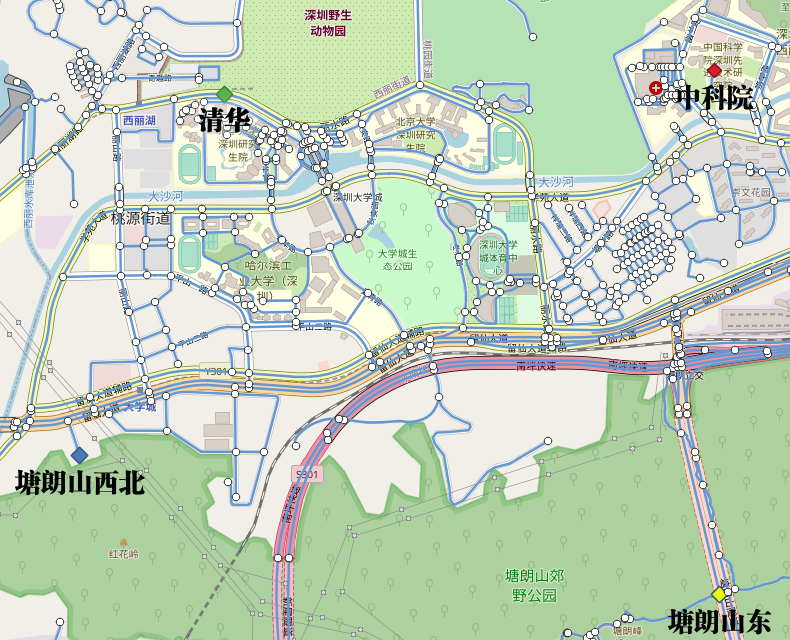
注：上述四个地方的拓扑 ID 不同电脑可能不同，需要针对自己创建的拓扑进行查看。

在确定 ID 时，一定满足最短路径分析函数的 source 和 target 要求，否则无结果。

4.1 基于行人的无向路径查询，考虑不同代价方式。

Ex1：单条行人路线（一到一）

从清华步行至中科院的最短距离，并用 QGIS
展示最短路径。从行人的角度看，图是无向的，即行人在所有路段上都可以沿道路的两个方向移动。行人的步行的代价按路线长度来衡量的（前面我们已经计算过路径的距离cost
和 reverse_cost）。

SELECT * FROM pgr_dijkstra(

'SELECT gid AS id,

source, target,

cost, reverse_cost

FROM shenzhen_roads',

59005, 59193,

directed := FALSE

);

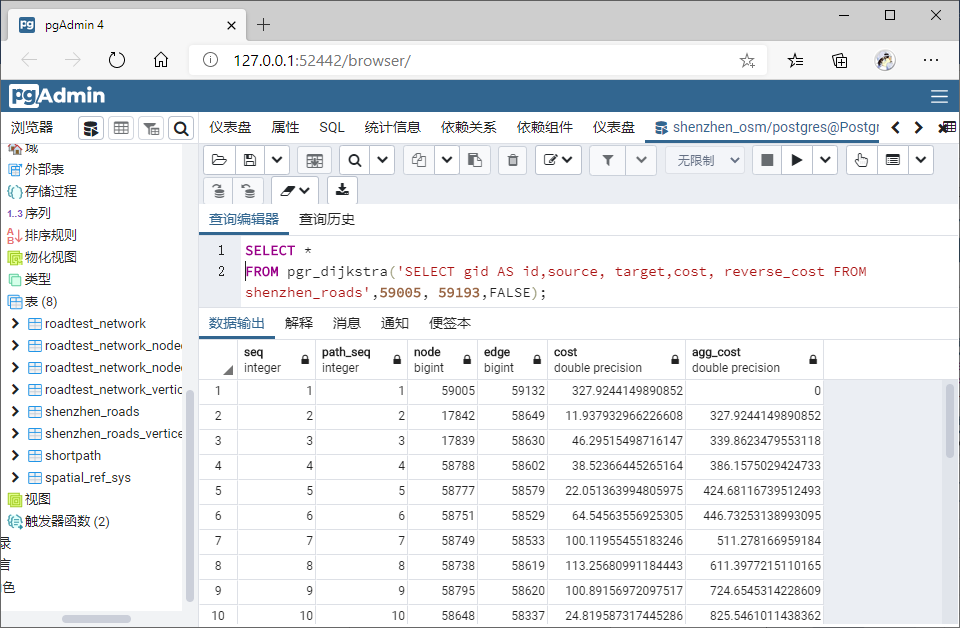
可视化：

QGIS 查看结果如下：

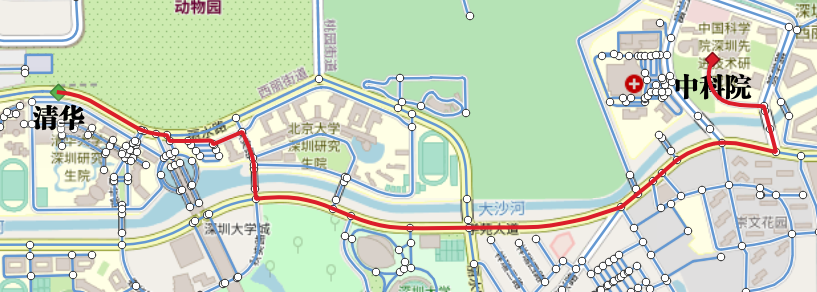
Ex2: 多个行人前往同一个目的地（多到一）

一个人从清华步行至中科院，另一个人从塘朗山郊野公园东步行至中科院，两人出发地不同，目的地一致。

SELECT * FROM pgr_dijkstra(

'SELECT gid AS id,

source, target,

cost, reverse_cost

FROM shenzhen_roads',

ARRAY[59005, 16177], 59193,

directed := FALSE

);

可视化：

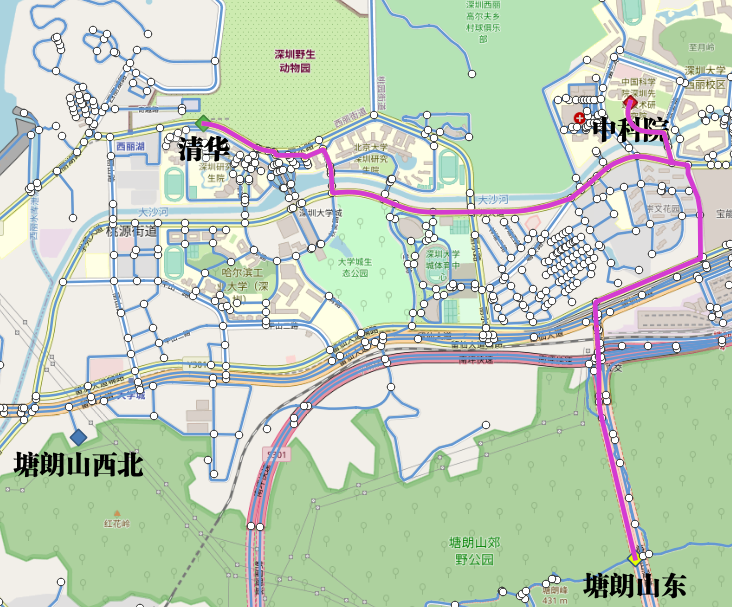
Ex3: 许多行人从同一地点离开（一到多）

两人分别从塘朗山郊野公园东离开，一个去清华，一个去中科院。使用行人的步行时间作为成本（以最短时间为佳），行人的步行速度为speed
= 1.3 m/s，所以步行时间time = distance / speed。

SELECT * FROM pgr_dijkstra(

'SELECT gid AS id,source, target,

cost/1.3 AS cost, reverse_cost/1.3 AS reverse_cost

FROM shenzhen_roads',

12089, ARRAY[10564, 13019],

directed := FALSE

);

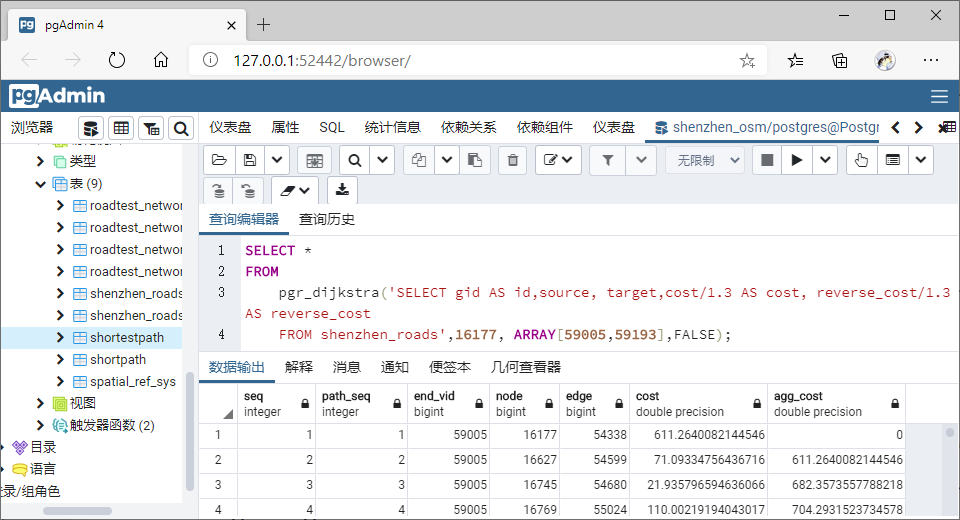
可视化：

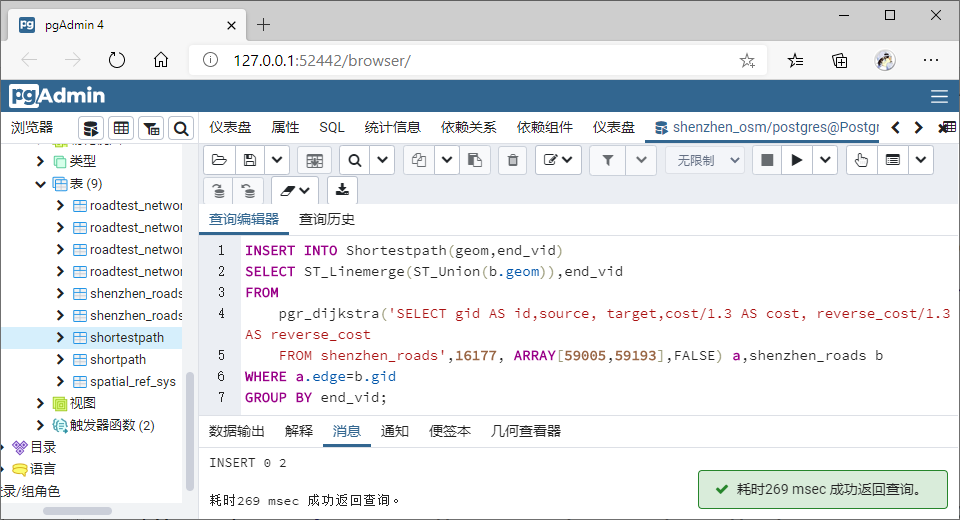
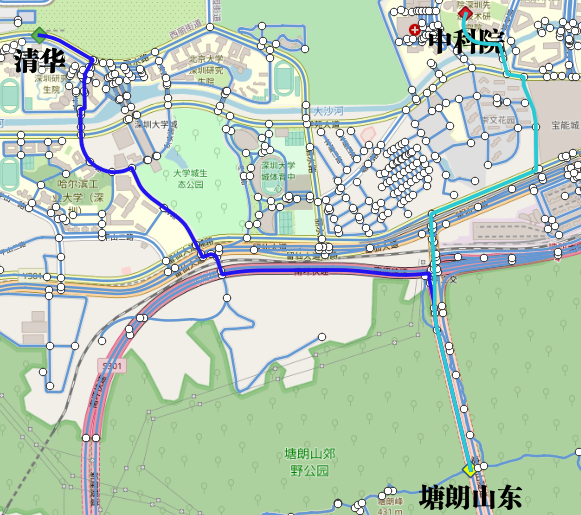
Ex4: 多个行人到不同的目的地（多到多）

两个同学，一个从清华出发去塘朗山郊野公园西和中科院，一个从中科院出发去清华和塘朗山郊野公园东。使用行人的步行时间作为权重（最短时间），不过单位是分钟。行人的步行速度为
speed = 1.3 m/s，所以步行时间t = distance / speed / 60mintues。

SELECT * FROM pgr_dijkstra(

'SELECT gid AS id,

source, target,

cost/1.3/60 AS cost, reverse_cost/1.3/60 AS reverse_cost

FROM shenzhen_roads',

ARRAY[59005, 59193], ARRAY[57059, 16177],

directed := FALSE

);

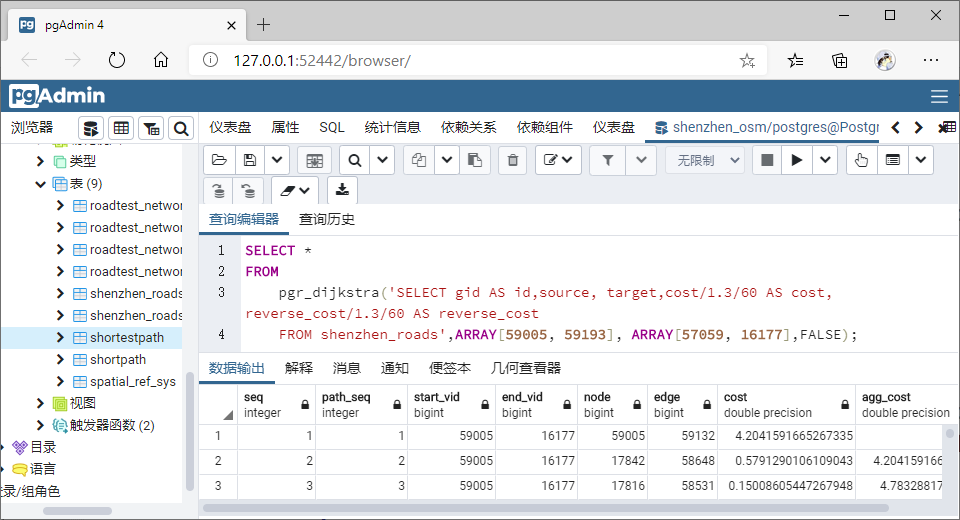
可视化：

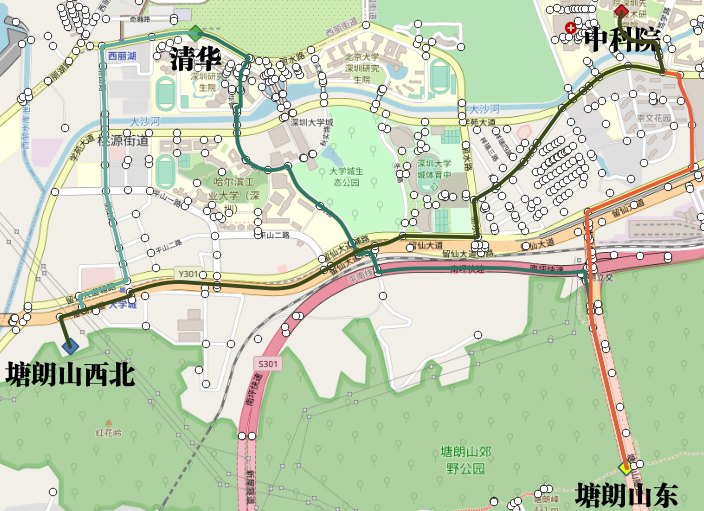
4.2 基于车辆的有向路径查询，考虑不同优先级方式。

【预备知识】车辆路径规划一般与行人路径规划不同：

①车辆道路是有方向的

②成本（代价）可以是：距离、时间、花销、二氧化碳排放量、车辆耗损等

③在双向道路上必须同时考虑cost 和reverse_cost 属性

成本应该和 cost 属性相同或和 reverse_cost 属性相同、同一条道路的cost 和
reverse_cost 可以是不同的这是因为有些道路是单向的。

单向道路的特征是：

(source, target)路段中，cost >= 0 且 reverse_cost < 0 (target,
source)路段中，cost < 0 且 reverse_cost >= 0

所以，用 cost 属性或 reverse_cost 属性的负值表示对应方向是无效的。

对于双向道路，cost >= 0 和reverse_cost >=
0，它们的值可能不同。例如，在一条倾斜的道路中，下山肯定比上山容易（或者更快）。成本可以是长度、时间、坡度、路面、道路类型等，也可以是多个参数的组合。

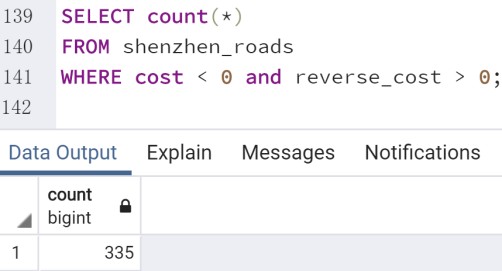
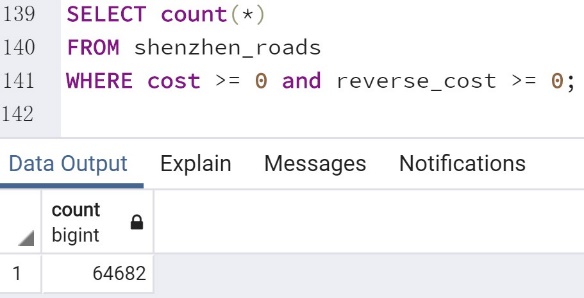
比如：深圳道路网中（source，target）单向路有 46168 条，（target，
source）单向路有 335 条，双向路有 64682 条：

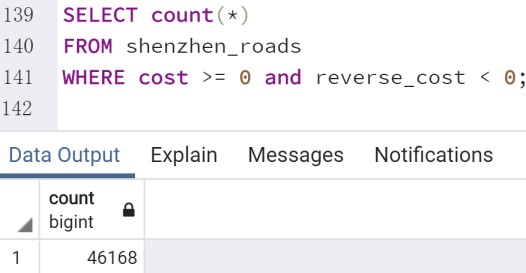
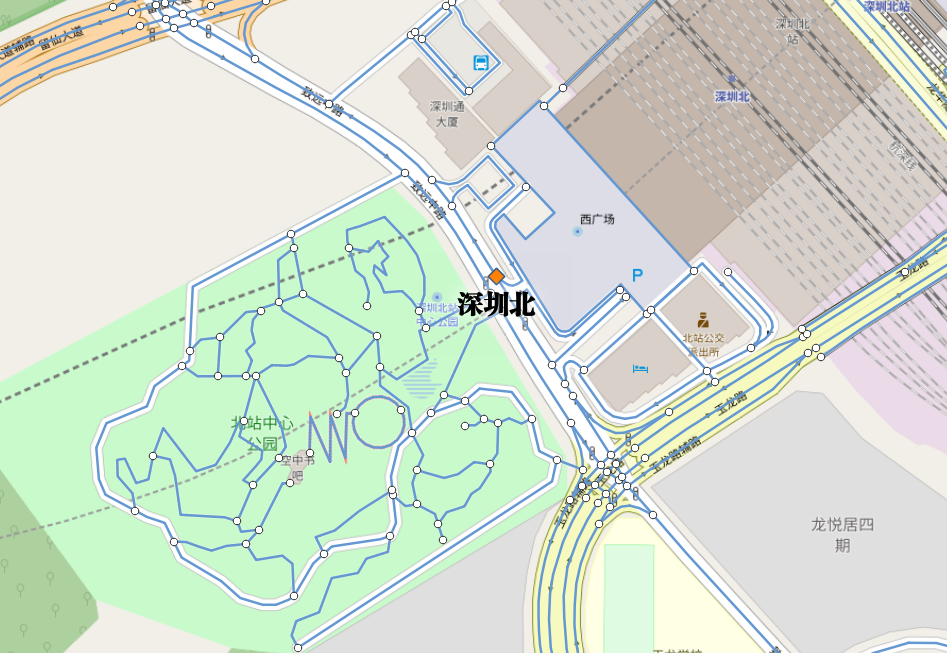
增加一个目的地：深圳北站（ID：19255）

（1）无优先级的路径规划

Ex1：行车路径（出发），从清华去深圳北站。

使用cost和reverse_cost列，它们的单位为米。

SELECT * FROM pgr_dijkstra(

'SELECT gid AS id,

source, target,

cost, reverse_cost

FROM shenzhen_roads

',

59005, 19255,

directed := true

);

可视化：

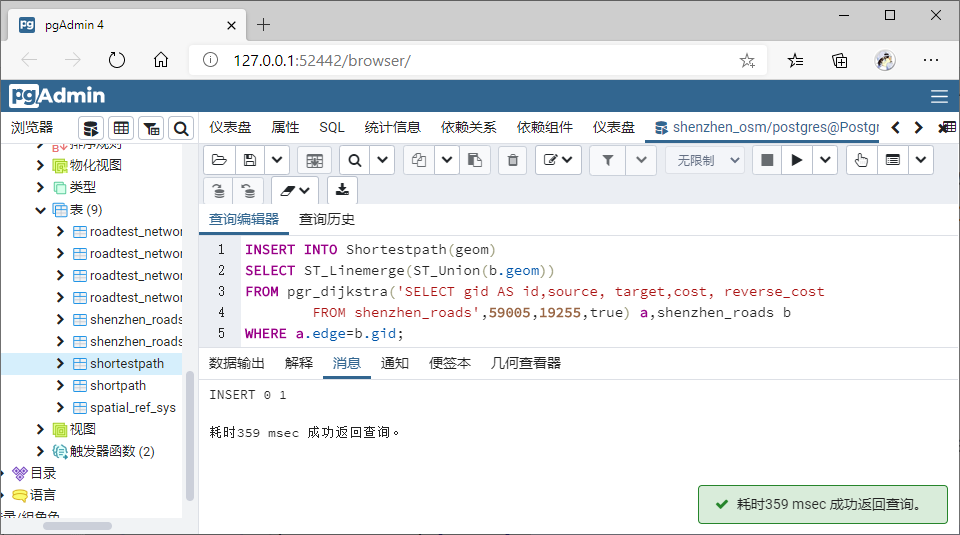
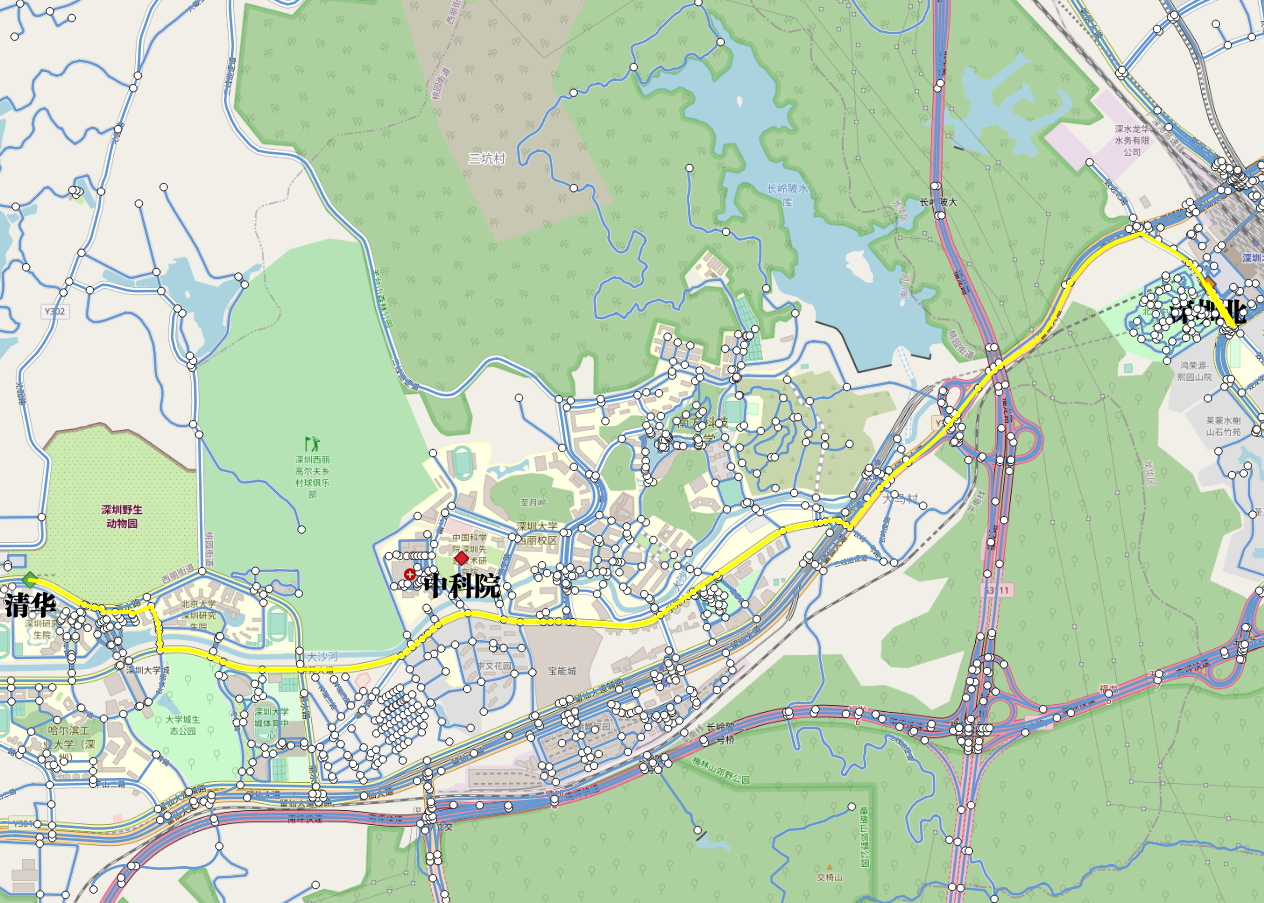
Ex2：行车路径（返回），从深圳北站回清华。

SELECT * FROM pgr_dijkstra(

'SELECT gid AS id,

source, target,

cost, reverse_cost

FROM shenzhen_roads

',

19255, 59005,

directed := true

);

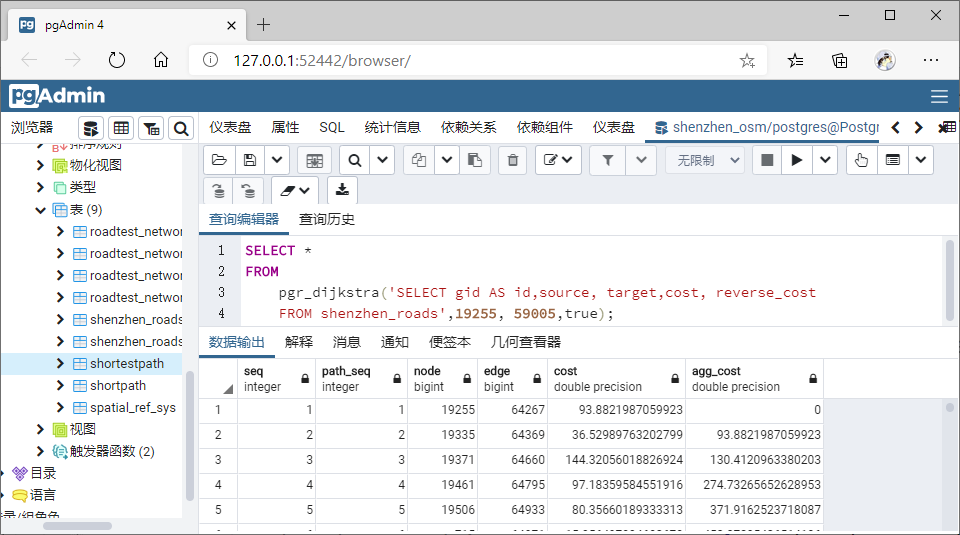
可视化

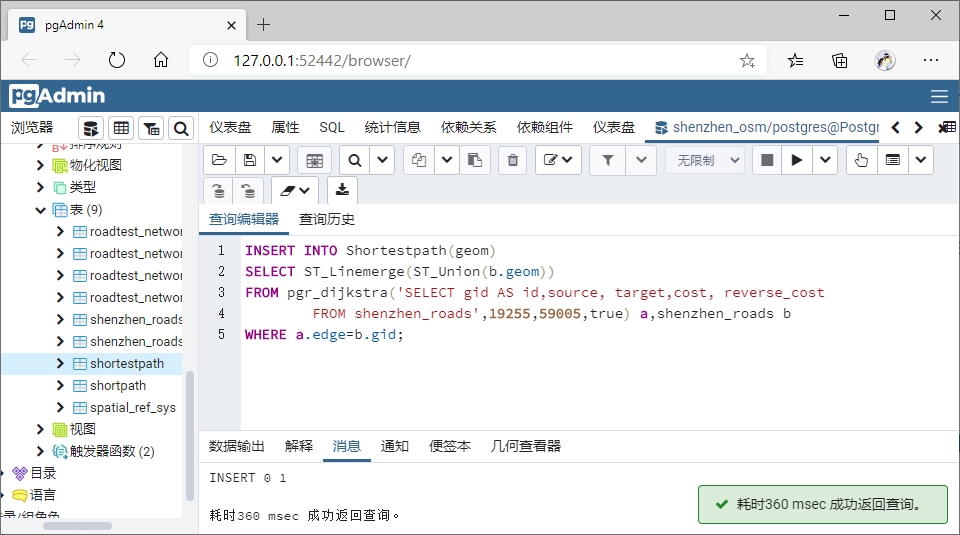
（2）具备优先级的道路路径规划问题

在处理数据时，了解所使用的数据类型可以顾及更多因素，从而得到更理想的结果。例如，如果我们知道某条路径是行人路径（pedestrian），就应该让车辆尽量避免或禁止在该路径上行驶。

因此，我们为道路表增加一列属性，去标记不同道路行走的优先级。

现在添加一个penalty 列用于保存每条路径的优先级信息（penalty
值越小，优先级越高）：

ALTER TABLE shenzhen_roads ADD COLUMN penalty DOUBLE PRECISION;

初始值都为 1.0，表明所有道路具备同等优先级别。

UPDATE shenzhen_roads SET penalty = 1.0;

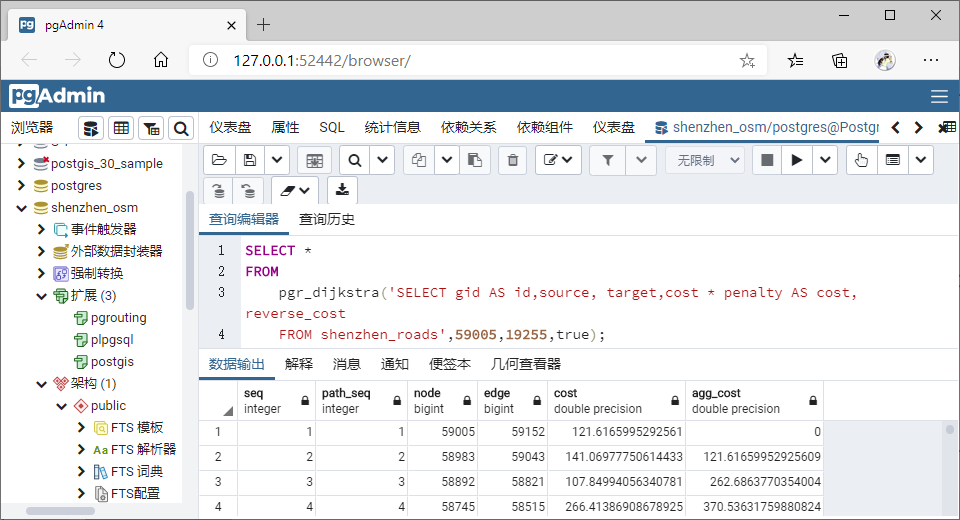
Ex3：基于无优先级路径查询乘车从清华至深圳北站（将 cost * penalty
作为正向路径成本）。

SELECT * FROM pgr_dijkstra(

'SELECT gid AS id,

source, target,

cost * penalty AS cost,

reverse_cost

FROM shenzhen_roads

',

59005, 19255,

directed := true

);

查询的结果路径和 Ex1 的结果路径一致：

Ex4：具有优先级路径查询乘车从清华至深圳北站。

因为业务场景是查找车辆的行驶路径，所以可以让路径的优先级符合以下规则：

• 禁止在pedestrian、footway、steps、cycleway、track这些路径上行驶。

• 不鼓励在rsidential路径上行驶。

• 鼓励在primary、primary_link路径上行驶。

修改路径的优先级具体如下：

UPDATE shenzhen_roads SET penalty **= -**1.0

WHERE fclass IN ('steps','footway','pedestrian', 'cycleway', 'track',
'track_grade2');

UPDATE shenzhen_roads SET penalty = 5.0

WHERE fclass IN ('residential');

UPDATE shenzhen_roads SET penalty = 0.8

WHERE fclass IN ('tertiary', 'tertiary_link', 'motorway',
'motorway_link', 'living_street');

UPDATE shenzhen_roads SET penalty = 0.5

WHERE fclass IN ('secondary', 'secondary_link');

UPDATE shenzhen_roads SET penalty = 0.3

WHERE fclass IN ('primary', 'primary_link', 'trunk', 'trunk_link');

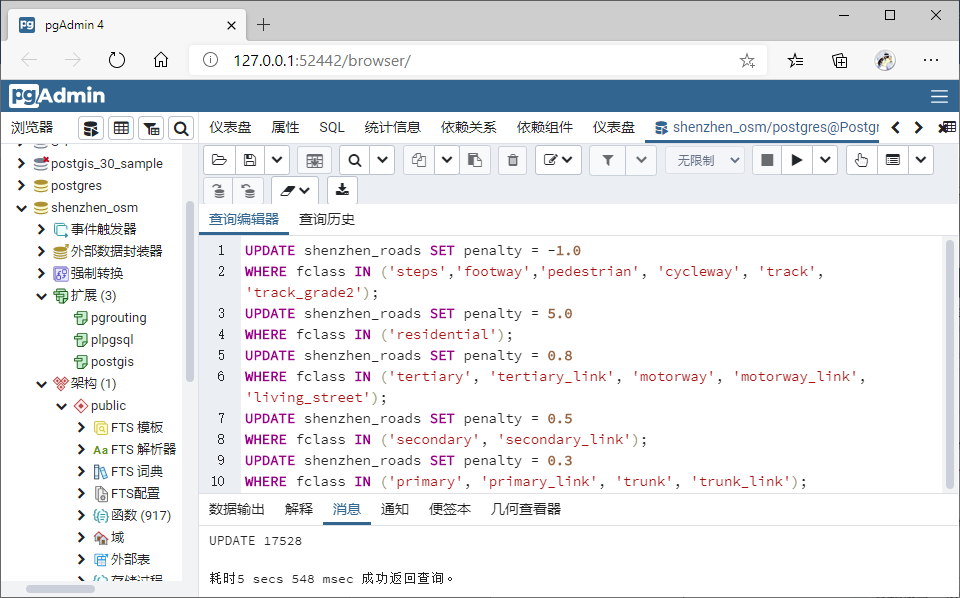
重新查询路径：

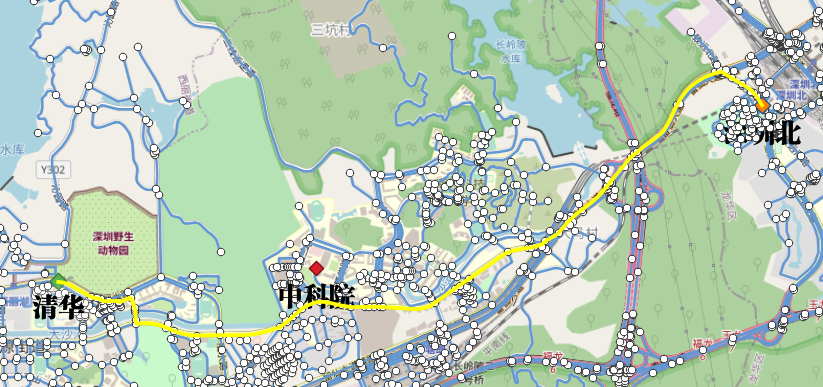
可视化：

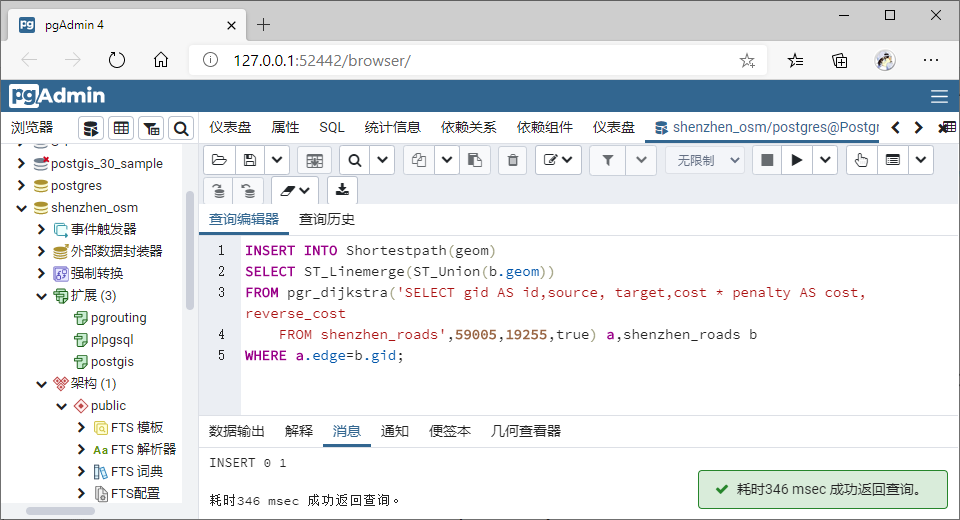
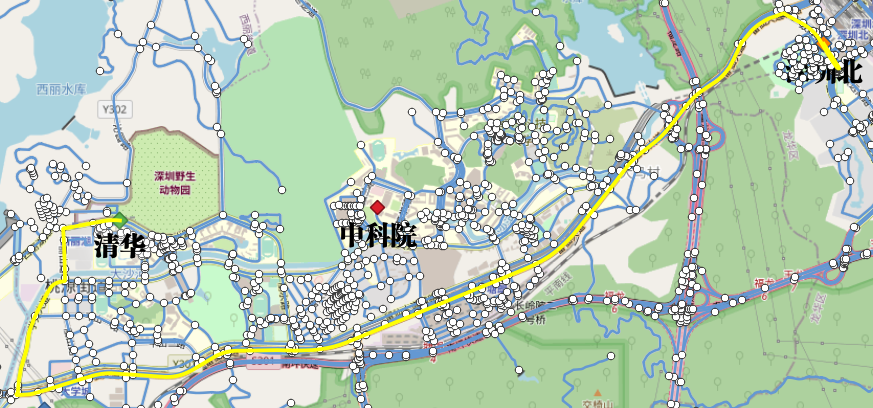
**4.3习题

某同学在塘朗山郊野公园，通过手机定位给你发送了一个位置信息（12688302.5,2580759.8@EPSG:3857），你当前在清华宿舍休息，如果你通过导航去找你同学（步行或自驾均可），请给出最优路径（考虑距离最短或耗时最短）。**

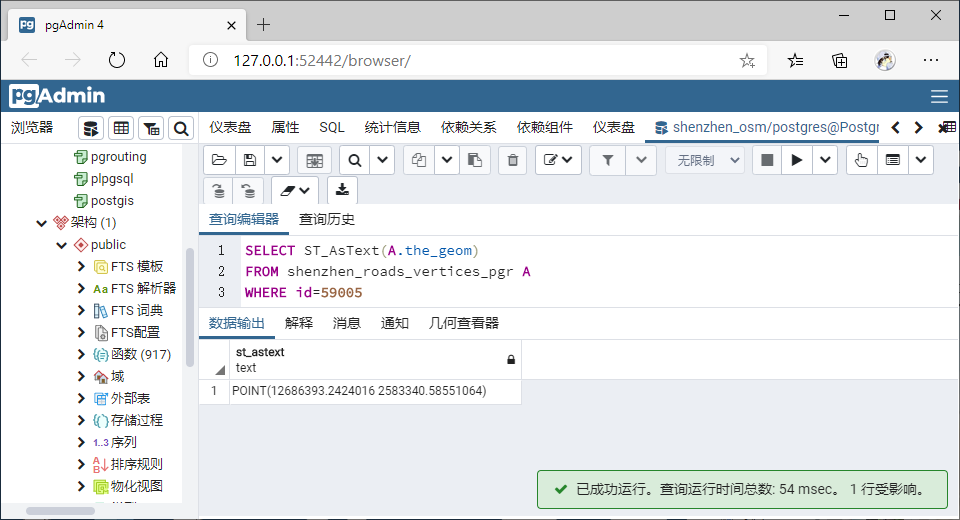
查询清华所在坐标

自定义函数

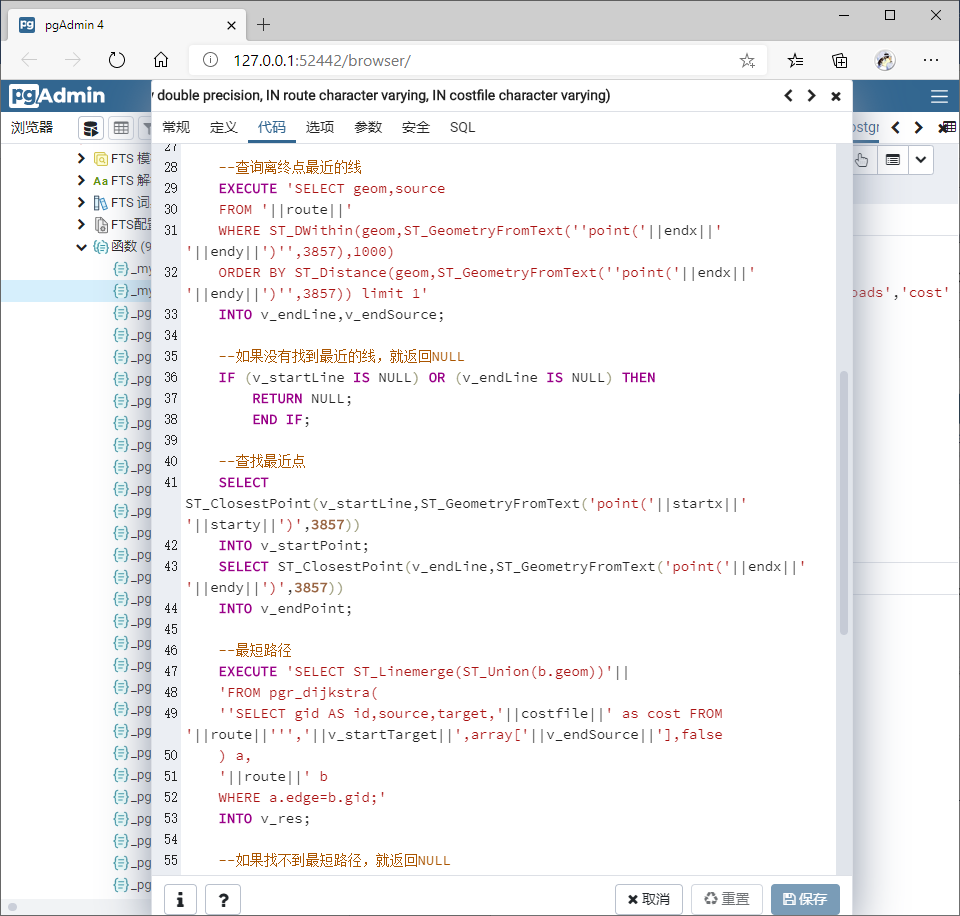
查询距离最短路径

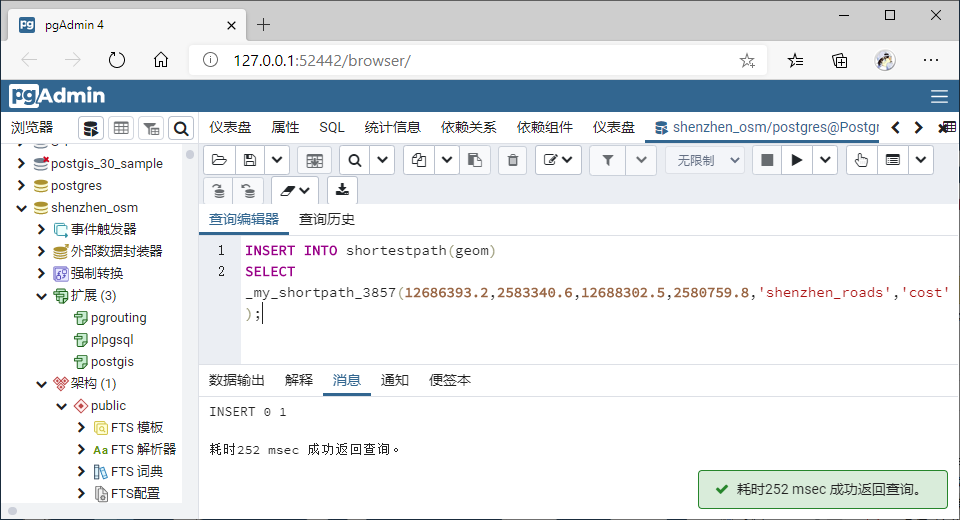
在QGIS中查看

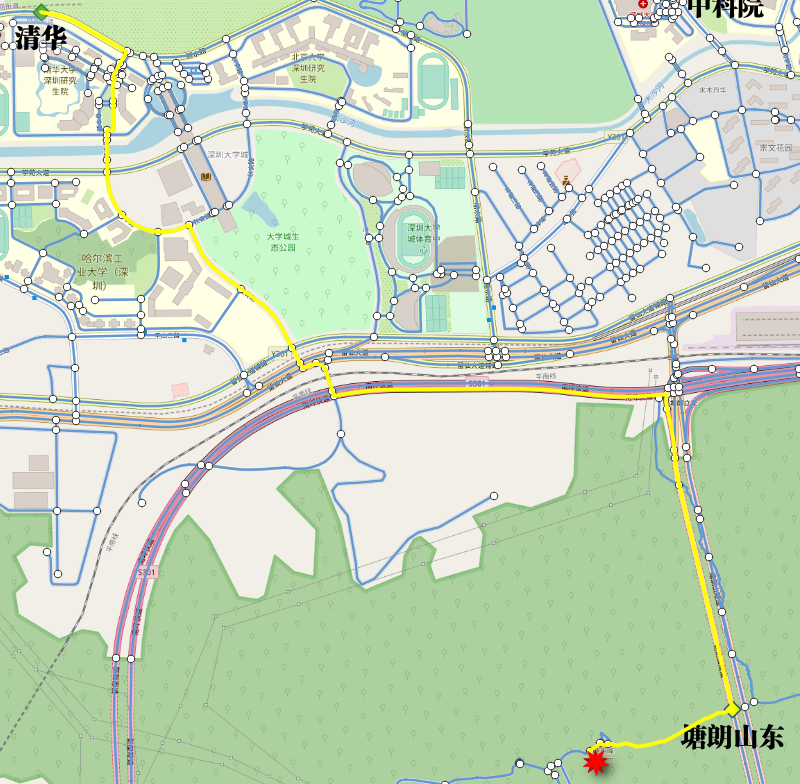
查询耗时最短路径

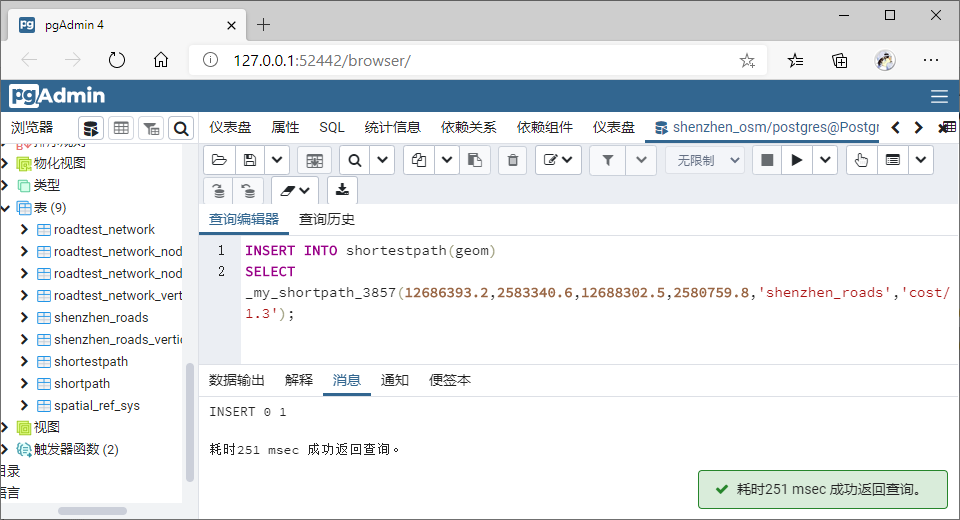
在QGIS中查看

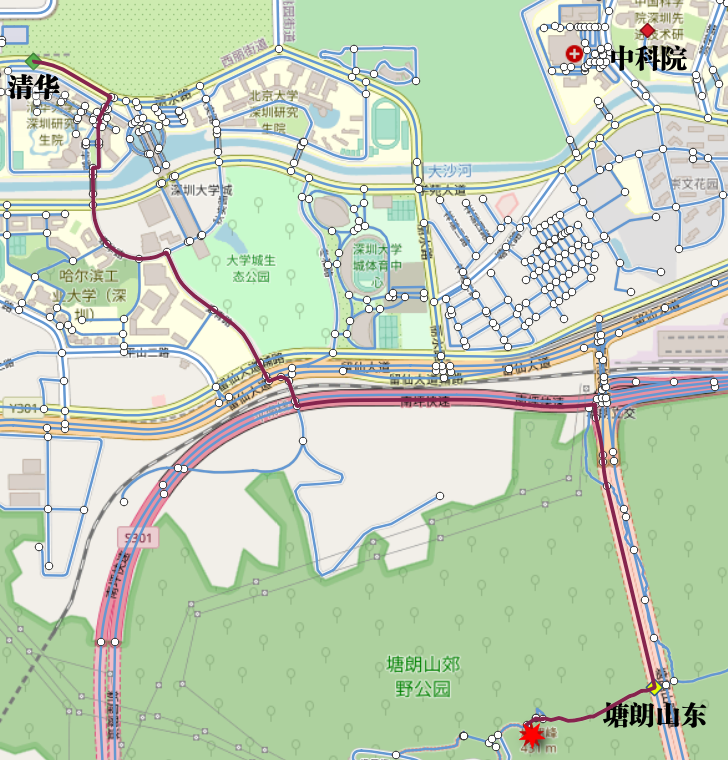
查询考虑道路优先级路径

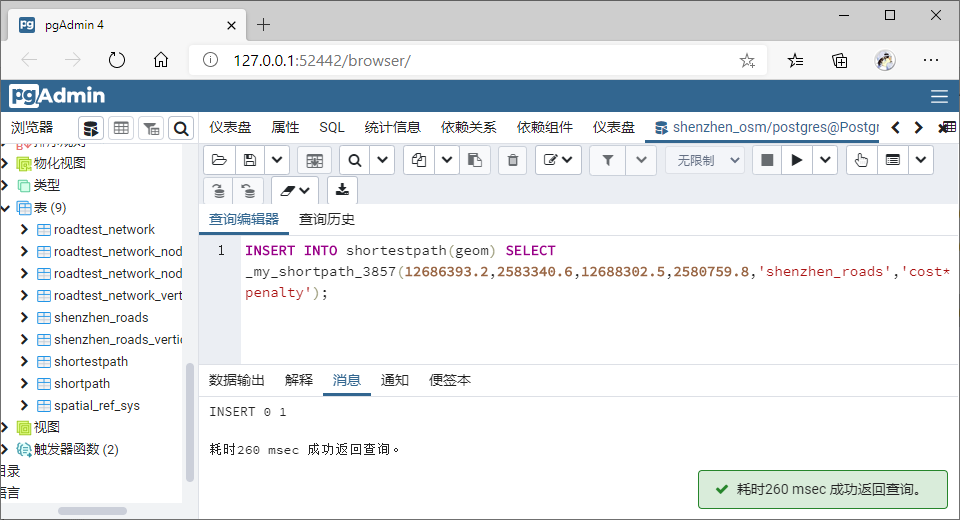
在QGIS中查看

SQL代码

--加载扩展
CREATE EXTENSION postgis;
CREATE EXTENSION pgrouting;

--创建表
CREATE TABLE Roadtest_Network (
	id serial PRIMARY KEY,
	name text,
	source integer,
	target integer,
	geom geometry(LineString, 4326),
	len double precision
	);

--插入数据	
INSERT INTO Roadtest_Network(id,name,geom)
VALUES
(1,'A',ST_GeomFromText('LineString(00 20, 10 20)',4326)),
(2,'B',ST_GeomFromText('LineString(10 20, 10 02)',4326)),
(3,'C',ST_GeomFromText('LineString(10 02, 20 02)',4326)),
(4,'D',ST_GeomFromText('LineString(00 05, 20 05)',4326)),
(5,'E',ST_GeomFromText('LineString(20 4.9999, 20 2.0001)',4326));
Update roadtest_network
Set len = ST_Length(geom);

--创建拓扑
SELECT pgr_createTopology('roadtest_network',0.00001,'geom','id','source','target','true');

--拓扑分析
SELECT pgr_analyzeGraph('roadtest_network',0.00001,'geom','id','source','target','true');

--节点重构
SELECT pgr_nodeNetwork('roadtest_network',0.00001,'id','geom','noded')

--基于重构的节点创建拓扑
SELECT pgr_createTopology('roadtest_network_noded',0.00001,'geom','id','source','target','true');

--进行新的拓扑分析
SELECT pgr_analyzeGraph('roadtest_network_noded',0.00001,'geom','id','source','target','true');

--更新表
DELETE FROM roadtest_network;
INSERT INTO roadtest_network(source,target,geom)
VALUES
(SELECT source,target,geom
FROM roadtest_network_noded);

--插入路F
INSERT INTO Roadtest_Network(id,name,geom)
VALUES
(8,'F',ST_GeomFromText('LineString(00 05, 10 20)',4326));
Update roadtest_network
Set len = ST_Length(geom);
SELECT pgr_createTopology('roadtest_network',0.00001,'geom','id','source','target','true');

--查询5-3最短路径
SELECT *
FROM pgr_dijkstra('SELECT id,source,target,len as cost FROM Roadtest_network',5,3,false);

--自定义函数
DECLARE
	v_startLine geometry;--离起点最近的线
	v_endLine geometry;--离终点最近的线
	
	v_startLine1 geometry;--出发点与拓扑起始节点的连线
	v_endLine1 geometry;--结束点与拓扑结束节点的连线
	
	v_startTarget integer;--距离起点最近线的终点
	v_endSource integer;--距离终点最近线的起点
	v_startPoint geometry;--在v_startLine上距离起点最近的点
	v_endPoint geometry;--在v_endLin上距离起点最近的点
	
	startPoint geometry;--出发点
	endPoint geometry;--结束点
	
	v_res geometry;--最短路径分析结果
	v_perStart float;--v_startPoint在v_res上的百分比
	v_perEnd float;--v_endPoint在v_res上的百分比
	v_shPath geometry;--最终结果
BEGIN
	--查询离起点最近的线
	EXECUTE 'SELECT geom,target
	FROM '||route||'
	WHERE ST_DWithin(geom,ST_GeometryFromText(''point('||startx||' '||starty||')'',4326),20)
	ORDER BY ST_Distance(geom,ST_GeometryFromText(''point('||startx||' '||starty||')'',4326)) limit 1'
	INTO v_startLine,v_startTarget;
	
	--查询离终点最近的线
	EXECUTE 'SELECT geom,source
	FROM '||route||'
	WHERE ST_DWithin(geom,ST_GeometryFromText(''point('||endx||' '||endy||')'',4326),20)
	ORDER BY ST_Distance(geom,ST_GeometryFromText(''point('||endx||' '||endy||')'',4326)) limit 1'
	INTO v_endLine,v_endSource;
	
	--如果没有找到最近的线，就返回NULL
	IF (v_startLine IS NULL) OR (v_endLine IS NULL) THEN
		RETURN NULL;
		END IF;
	
	--查找最近点
	SELECT ST_ClosestPoint(v_startLine,ST_GeometryFromText('point('||startx||' '||starty||')',4326))
	INTO v_startPoint;
	SELECT ST_ClosestPoint(v_endLine,ST_GeometryFromText('point('||endx||' '||endy||')',4326))
	INTO v_endPoint;
	
	--最短路径
	EXECUTE 'SELECT ST_Linemerge(ST_Union(b.geom))'||
	'FROM pgr_dijkstra(
	''SELECT id,source,target,'||costfile||' as cost FROM '||route||''','||v_startTarget||',array['||v_endSource||'],false
	) a,
	'||route||' b
	WHERE a.edge=b.id;'
	INTO v_res;
	
	--如果找不到最短路径，就返回NULL
	IF(v_res IS NULL) THEN
		RETURN NULL;
		END IF;
	
	--将v_res,v_startLine,v_endLine进行拼接
	SELECT ST_Linemerge(ST_Union(array[v_res,v_startLine,v_endLine])) INTO v_res;
	SELECT ST_LineLocatePoint(v_res,v_startPoint) INTO v_perStart;
	SELECT ST_LineLocatePoint(v_res,v_endPoint) INTO v_perEnd;
	
	--截取v_res
	SELECT ST_SetSRID(ST_MakePoint(startx,starty),4326) INTO startPoint;
	SELECT ST_SetSRID(ST_MakePoint(endx,endy),4326) INTO endPoint;
	
	IF V_perStart < V_perEnd THEN
	SELECT ST_LineSubString(v_res,v_perStart,v_perEnd) INTO v_shPath;
	SELECT ST_MakeLine(ST_StartPoint(v_shPath),startpoint) INTO v_startLine1;
	SELECT ST_MakeLine(ST_EndPoint(v_shPath),endpoint) INTO v_endLine1;
	ELSE      
	SELECT ST_LineSubString(v_res,V_perEnd,v_perStart) INTO v_shPath; 
	SELECT ST_MakeLine(ST_EndPoint(v_shPath),startpoint) INTO v_startLine1;
	SELECT ST_MakeLine(ST_StartPoint(v_shPath),endpoint) INTO v_endLine1;
	END IF;
	
	SELECT ST_Union(array[v_shPath,v_startLine1,v_endLine1]) INTO v_shPath;
	
	RETURN v_shPath;
	
END;

--查询最短路线
CREATE TABLE shortpath(
	ID serial PRIMARY KEY,
	geom geometry(MultiLineString, 4326) 
	);
INSERT INTO shortpath(geom) SELECT _my_shortpath(12,06,10,20,'roadtest_network','len');
INSERT INTO shortpath(geom) SELECT _my_shortpath(12,06,18,04,'roadtest_network','len');


--添加字段
ALTER TABLE shenzhen_roads
ADD COLUMN source INTEGER,
ADD COLUMN target INTEGER,
ADD COLUMN cost DOUBLE PRECISION,
ADD COLUMN reverse_cost DOUBLE PRECISION;
--①正向路径的成本：
UPDATE shenzhen_roads
SET cost = ST_Length(geom),
reverse_cost = -1
WHERE oneway = 'F';

--②反向路径的成本：
UPDATE shenzhen_roads
SET cost = -1,
reverse_cost = ST_Length(geom)
WHERE oneway = 'T';

--③双向路径的成本：
UPDATE shenzhen_roads
SET cost = ST_Length(geom),
reverse_cost = ST_Length(geom)
WHERE oneway = 'B';

--创建拓扑
SELECT pgr_createTopology(
	'shenzhen_roads', 
	0.001,
	'geom',
	'gid',
	'source',
	'target'
); 
--拓扑查错
SELECT pgr_analyzeGraph('shenzhen_roads',0.001,'geom','gid','source','target');

--4.1.1
SELECT *
FROM
	pgr_dijkstra('SELECT gid AS id,source, target,cost, reverse_cost
	FROM shenzhen_roads',59005, 59193,FALSE);

CREATE TABLE Shortestpath(
	ID serial PRIMARY KEY,
	start_vid bigint,
	end_vid bigint,
	geom geometry(LineString,3857) 
	);
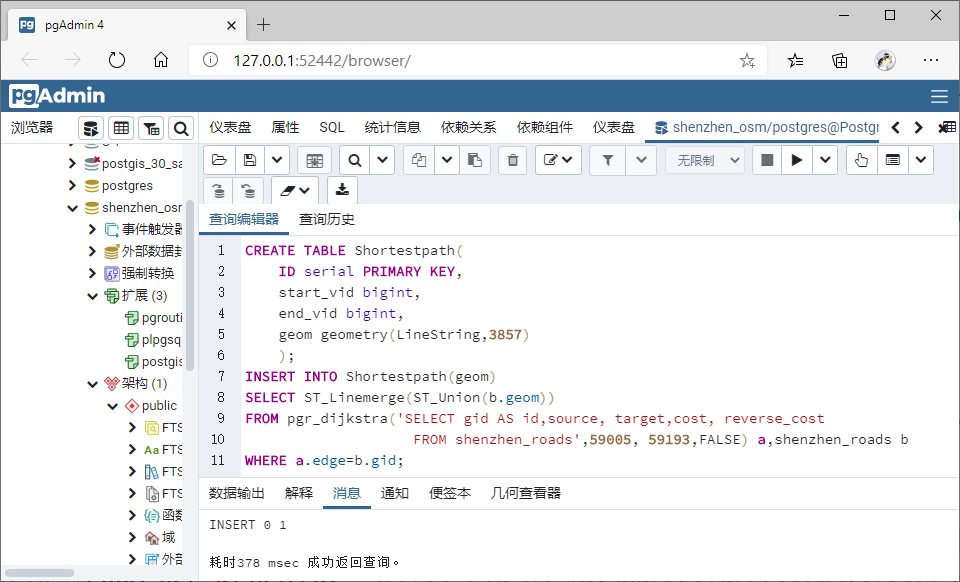
INSERT INTO Shortestpath(geom)
SELECT ST_Linemerge(ST_Union(b.geom))
FROM pgr_dijkstra('SELECT gid AS id,source, target,cost, reverse_cost 
					FROM shenzhen_roads',59005, 59193,FALSE) a,shenzhen_roads b
WHERE a.edge=b.gid;

--4.1.2
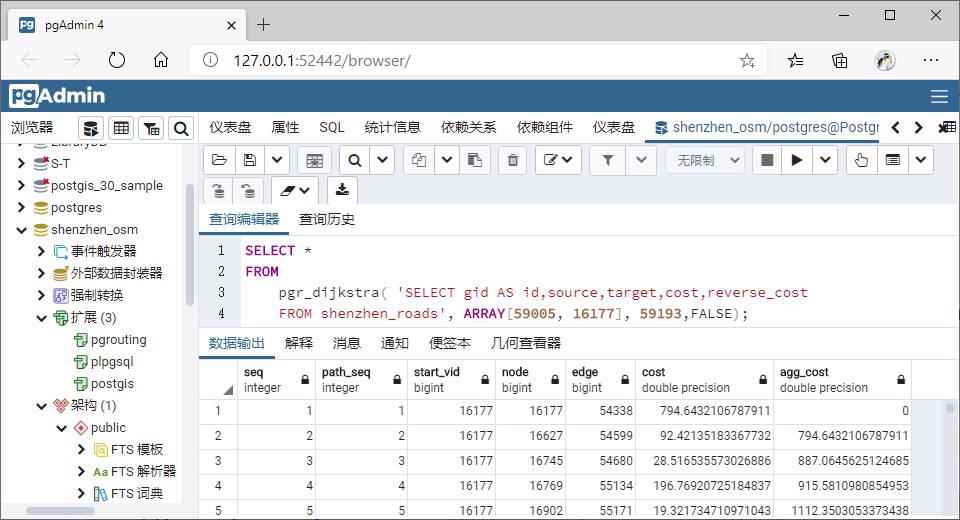
SELECT *
FROM
	pgr_dijkstra( 'SELECT gid AS id,source,target,cost,reverse_cost
	FROM shenzhen_roads', ARRAY[59005, 16177], 59193,FALSE);
	
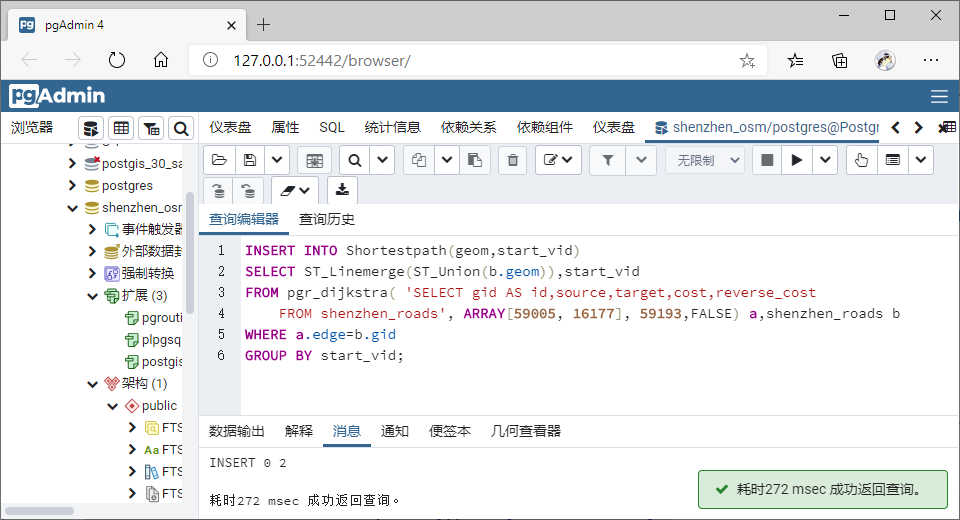
INSERT INTO Shortestpath(geom,start_vid)
SELECT ST_Linemerge(ST_Union(b.geom)),start_vid 
FROM pgr_dijkstra( 'SELECT gid AS id,source,target,cost,reverse_cost
	FROM shenzhen_roads', ARRAY[59005, 16177], 59193,FALSE) a,shenzhen_roads b
WHERE a.edge=b.gid
GROUP BY start_vid;

--4.1.3
SELECT * 
FROM 
	pgr_dijkstra('SELECT gid AS id,source, target,cost/1.3 AS cost, reverse_cost/1.3 AS reverse_cost
	FROM shenzhen_roads',16177, ARRAY[59005,59193],FALSE);

INSERT INTO Shortestpath(geom,end_vid)
SELECT ST_Linemerge(ST_Union(b.geom)),end_vid
FROM 
	pgr_dijkstra('SELECT gid AS id,source, target,cost/1.3 AS cost, reverse_cost/1.3 AS reverse_cost
	FROM shenzhen_roads',16177, ARRAY[59005,59193],FALSE) a,shenzhen_roads b
WHERE a.edge=b.gid
GROUP BY end_vid; 

--4.1.4
SELECT * 
FROM 
	pgr_dijkstra('SELECT gid AS id,source, target,cost/1.3/60 AS cost, reverse_cost/1.3/60 AS reverse_cost
	FROM shenzhen_roads',ARRAY[59005, 59193], ARRAY[57059, 16177],FALSE);
	
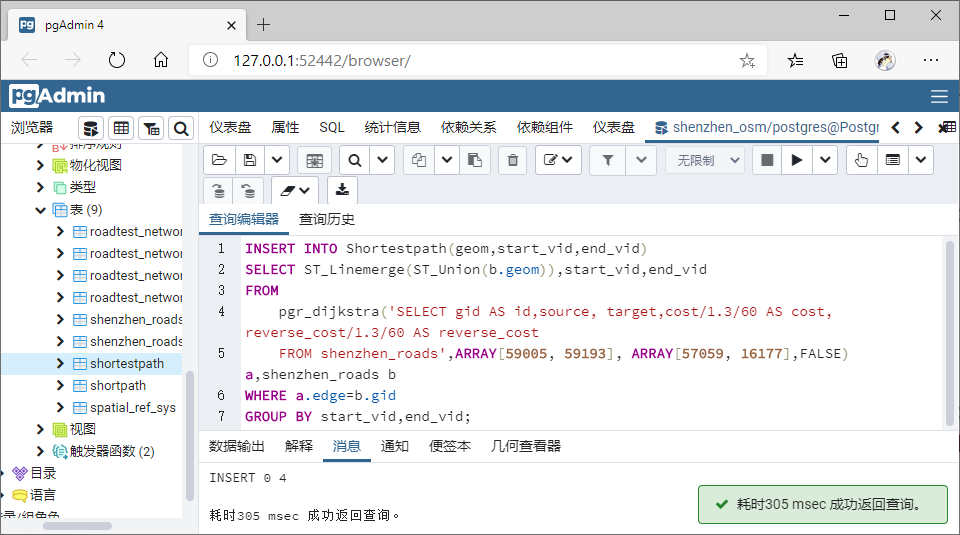
INSERT INTO Shortestpath(geom,start_vid,end_vid)
SELECT ST_Linemerge(ST_Union(b.geom)),start_vid,end_vid
FROM 
	pgr_dijkstra('SELECT gid AS id,source, target,cost/1.3/60 AS cost, reverse_cost/1.3/60 AS reverse_cost
	FROM shenzhen_roads',ARRAY[59005, 59193], ARRAY[57059, 16177],FALSE) a,shenzhen_roads b
WHERE a.edge=b.gid
GROUP BY start_vid,end_vid; 

--4.2.1
SELECT * 
FROM 
	pgr_dijkstra('SELECT gid AS id,source, target,cost, reverse_cost
	FROM shenzhen_roads',59005, 19255,true);

INSERT INTO Shortestpath(geom)
SELECT ST_Linemerge(ST_Union(b.geom))
FROM pgr_dijkstra('SELECT gid AS id,source, target,cost, reverse_cost 
		FROM shenzhen_roads',59005,19255,true) a,shenzhen_roads b
WHERE a.edge=b.gid;

--4.2.2
SELECT * 
FROM 
	pgr_dijkstra('SELECT gid AS id,source, target,cost, reverse_cost
	FROM shenzhen_roads',19255, 59005,true);

INSERT INTO Shortestpath(geom)
SELECT ST_Linemerge(ST_Union(b.geom))
FROM pgr_dijkstra('SELECT gid AS id,source, target,cost, reverse_cost 
		FROM shenzhen_roads',19255,59005,true) a,shenzhen_roads b
WHERE a.edge=b.gid;

--4.2.3
SELECT * 
FROM 
	pgr_dijkstra('SELECT gid AS id,source, target,cost * penalty AS cost, reverse_cost
	FROM shenzhen_roads',59005,19255,true);
	
--4.2.4
UPDATE shenzhen_roads SET penalty = -1.0
WHERE fclass IN ('steps','footway','pedestrian', 'cycleway', 'track', 'track_grade2');

UPDATE shenzhen_roads SET penalty = 5.0
WHERE fclass IN ('residential');

UPDATE shenzhen_roads SET penalty = 0.8
WHERE fclass IN ('tertiary', 'tertiary_link', 'motorway', 'motorway_link', 'living_street');
UPDATE shenzhen_roads SET penalty = 0.5
WHERE fclass IN ('secondary', 'secondary_link');

UPDATE shenzhen_roads SET penalty = 0.3
WHERE fclass IN ('primary', 'primary_link', 'trunk', 'trunk_link');

SELECT * 
FROM 
	pgr_dijkstra('SELECT gid AS id,source, target,cost * penalty AS cost, reverse_cost
	FROM shenzhen_roads',59005,19255,true);
INSERT INTO Shortestpath(geom)
SELECT ST_Linemerge(ST_Union(b.geom))
FROM pgr_dijkstra('SELECT gid AS id,source, target,cost * penalty AS cost, reverse_cost
	FROM shenzhen_roads',59005,19255,true) a,shenzhen_roads b
WHERE a.edge=b.gid;

--

DECLARE
	v_startLine geometry;--离起点最近的线
	v_endLine geometry;--离终点最近的线
	
	v_startLine1 geometry;--出发点与拓扑起始节点的连线
	v_endLine1 geometry;--结束点与拓扑结束节点的连线
	
	v_startTarget integer;--距离起点最近线的终点
	v_endSource integer;--距离终点最近线的起点
	v_startPoint geometry;--在v_startLine上距离起点最近的点
	v_endPoint geometry;--在v_endLin上距离起点最近的点
	
	startPoint geometry;--出发点
	endPoint geometry;--结束点
	
	v_res geometry;--最短路径分析结果
	v_perStart float;--v_startPoint在v_res上的百分比
	v_perEnd float;--v_endPoint在v_res上的百分比
	v_shPath geometry;--最终结果
BEGIN
	--查询离起点最近的线
	EXECUTE 'SELECT geom,target
	FROM '||route||'
	WHERE ST_DWithin(geom,ST_GeometryFromText(''point('||startx||' '||starty||')'',3857),1000)
	ORDER BY ST_Distance(geom,ST_GeometryFromText(''point('||startx||' '||starty||')'',3857)) limit 1'
	INTO v_startLine,v_startTarget;
	
	--查询离终点最近的线
	EXECUTE 'SELECT geom,source
	FROM '||route||'
	WHERE ST_DWithin(geom,ST_GeometryFromText(''point('||endx||' '||endy||')'',3857),1000)
	ORDER BY ST_Distance(geom,ST_GeometryFromText(''point('||endx||' '||endy||')'',3857)) limit 1'
	INTO v_endLine,v_endSource;
	
	--如果没有找到最近的线，就返回NULL
	IF (v_startLine IS NULL) OR (v_endLine IS NULL) THEN
		RETURN NULL;
		END IF;
	
	--查找最近点
	SELECT ST_ClosestPoint(v_startLine,ST_GeometryFromText('point('||startx||' '||starty||')',3857))
	INTO v_startPoint;
	SELECT ST_ClosestPoint(v_endLine,ST_GeometryFromText('point('||endx||' '||endy||')',3857))
	INTO v_endPoint;
	
	--最短路径
	EXECUTE 'SELECT ST_Linemerge(ST_Union(b.geom))'||
	'FROM pgr_dijkstra(
	''SELECT gid AS id,source,target,'||costfile||' as cost FROM '||route||''','||v_startTarget||',array['||v_endSource||'],false
	) a,
	'||route||' b
	WHERE a.edge=b.gid;'
	INTO v_res;
	
	--如果找不到最短路径，就返回NULL
	IF(v_res IS NULL) THEN
		RETURN NULL;
		END IF;
	
	--将v_res,v_startLine,v_endLine进行拼接
	SELECT ST_Linemerge(ST_Union(array[v_res,v_startLine,v_endLine])) INTO v_res;
	SELECT ST_LineLocatePoint(v_res,v_startPoint) INTO v_perStart;
	SELECT ST_LineLocatePoint(v_res,v_endPoint) INTO v_perEnd;
	
	--截取v_res
	SELECT ST_SetSRID(ST_MakePoint(startx,starty),3857) INTO startPoint;
	SELECT ST_SetSRID(ST_MakePoint(endx,endy),3857) INTO endPoint;
	
	IF V_perStart < V_perEnd THEN
	SELECT ST_LineSubString(v_res,v_perStart,v_perEnd) INTO v_shPath;
	SELECT ST_MakeLine(ST_StartPoint(v_shPath),startpoint) INTO v_startLine1;
	SELECT ST_MakeLine(ST_EndPoint(v_shPath),endpoint) INTO v_endLine1;
	ELSE      
	SELECT ST_LineSubString(v_res,V_perEnd,v_perStart) INTO v_shPath; 
	SELECT ST_MakeLine(ST_EndPoint(v_shPath),startpoint) INTO v_startLine1;
	SELECT ST_MakeLine(ST_StartPoint(v_shPath),endpoint) INTO v_endLine1;
	END IF;
	
	SELECT ST_Linemerge(ST_Union(array[v_shPath,v_startLine1,v_endLine1])) INTO v_shPath;
	
	RETURN v_shPath;
	
END;

INSERT INTO shortestpath(geom) SELECT _my_shortpath_3857(12686393.2,2583340.6,12688302.5,2580759.8,'shenzhen_roads','cost');
INSERT INTO shortestpath(geom) SELECT _my_shortpath_3857(12686393.2,2583340.6,12688302.5,2580759.8,'shenzhen_roads','cost/1.3'); 
INSERT INTO shortestpath(geom) SELECT _my_shortpath_3857(12686393.2,2583340.6,12688302.5,2580759.8,'shenzhen_roads','cost* penalty');